Dans ce chapitre, on se place dans un plan.
I – Projeté orthogonal
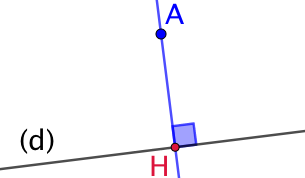 Soient
Soient Dans l’exemple de droite, ![]() est le projeté de
est le projeté de ![]() sur
sur ![]() .
.
Autrement dit : la distance ![]() est la plus petite distance entre
est la plus petite distance entre ![]() et un point de la droite
et un point de la droite ![]() .
. ![]() est le point de
est le point de ![]() le plus proche de
le plus proche de ![]() .
.
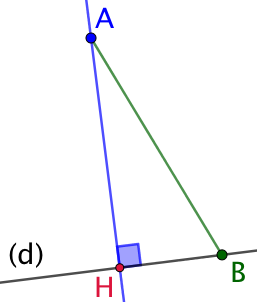 Démonstration : Soit
Démonstration : Soit ![]() un point quelconque de
un point quelconque de ![]() .
.
Par construction le triangle ![]() est rectangle en
est rectangle en ![]() . Le théorème de Pythagore appliqué à
. Le théorème de Pythagore appliqué à ![]() donne :
donne : ![]() .
.
Comme ![]() ,
, ![]() , donc
, donc ![]()
La fonction racine carrée est strictement croissante donc ![]() . Ce qui permet de conclure que
. Ce qui permet de conclure que ![]() .
.
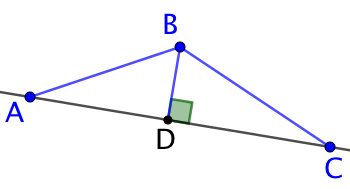 1ère partie : Soient trois points
1ère partie : Soient trois points ![]() ,
, ![]() et
et ![]() non alignés. Posons
non alignés. Posons ![]() le projeté orthogonal de
le projeté orthogonal de ![]() sur la droite
sur la droite ![]() .
.
Alors : ![]() et
et ![]() . Donc :
. Donc : ![]()
![]() ,
, ![]() et
et ![]() sont alignés donc
sont alignés donc ![]() . Par conséquent
. Par conséquent ![]() .
.
2ème partie : Supposons que ![]() et démontrons que les points
et démontrons que les points ![]() ,
, ![]() et
et ![]() ne sont pas alignés. On raisonne par l’absurde : supposons que ces points soient alignés.
ne sont pas alignés. On raisonne par l’absurde : supposons que ces points soient alignés.
Alors on aurait l’égalité : ![]() . Or on a supposé que
. Or on a supposé que ![]() . Notre raisonnement aboutit à une contradiction. Cela signifie que notre hypothèse « les trois points sont alignés » était fausse. Conclusion : ils ne sont pas alignés.
. Notre raisonnement aboutit à une contradiction. Cela signifie que notre hypothèse « les trois points sont alignés » était fausse. Conclusion : ils ne sont pas alignés.
II – Médiatrice d’un segment
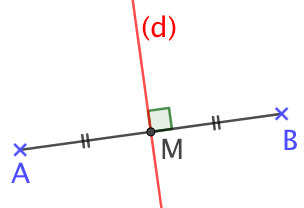 Dans l’exemple de droite, (d) est la médiatrice de [AB].
Dans l’exemple de droite, (d) est la médiatrice de [AB].
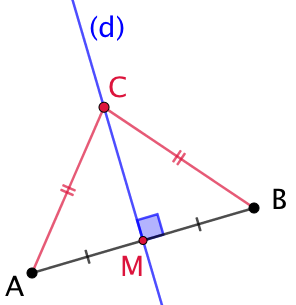 1ère partie : Soient (d) la médiatrice de [AB] et C un point de celle-ci. En appliquant le théorème de Pythagore aux triangles AMC et BMC, il vient d’une part que
1ère partie : Soient (d) la médiatrice de [AB] et C un point de celle-ci. En appliquant le théorème de Pythagore aux triangles AMC et BMC, il vient d’une part que ![]() et d’autre part que
et d’autre part que ![]() .
.
Or M est le milieu de [AB], donc ![]() . On en conclut que
. On en conclut que ![]() donc que
donc que ![]() . Le point C est bien équidistant de A et de B.
. Le point C est bien équidistant de A et de B.
2ème partie (réciproque) : Supposons que C soit un point équidistant de A et de B. Alors ![]() . Par ailleurs
. Par ailleurs ![]() . Donc les triangles AMC et BMC ont trois côtés de même longueur deux à deux. Ils sont donc isométriques (superposables).
. Donc les triangles AMC et BMC ont trois côtés de même longueur deux à deux. Ils sont donc isométriques (superposables).
Leurs trois angles sont par conséquent deux à deux de même mesure. En particulier ![]() . Les droites (AB) et (CM) étant sécantes en M et formant deux angles adjacents de même mesure, sont nécessairement perpendiculaires. Donc (CM) est la médiatrice de [AB] et se confond avec (d). Conclusion
. Les droites (AB) et (CM) étant sécantes en M et formant deux angles adjacents de même mesure, sont nécessairement perpendiculaires. Donc (CM) est la médiatrice de [AB] et se confond avec (d). Conclusion ![]() .
.
III – Triangles
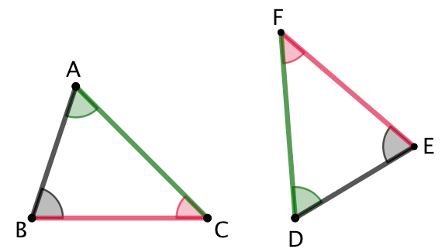 Exemple : les triangles ABC et DEF sont isométriques.
Exemple : les triangles ABC et DEF sont isométriques.
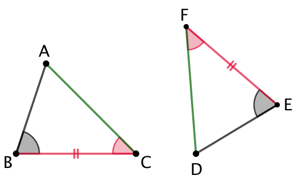 Exemple :
Exemple :
![]()
Donc les deux triangles sont isométriques.
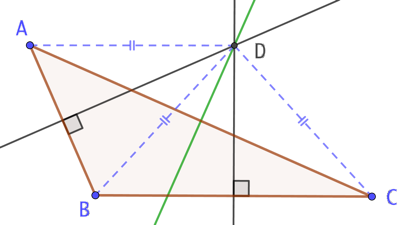 Les médiatrices d’un triangles sont au nombre de 3, une pour chaque côté du triangle.
Les médiatrices d’un triangles sont au nombre de 3, une pour chaque côté du triangle.
Dans l’exemple de droite, les trois médiatrices du triangle ABC se coupent au point D.
Pour lire la démonstration, cliquez ici.
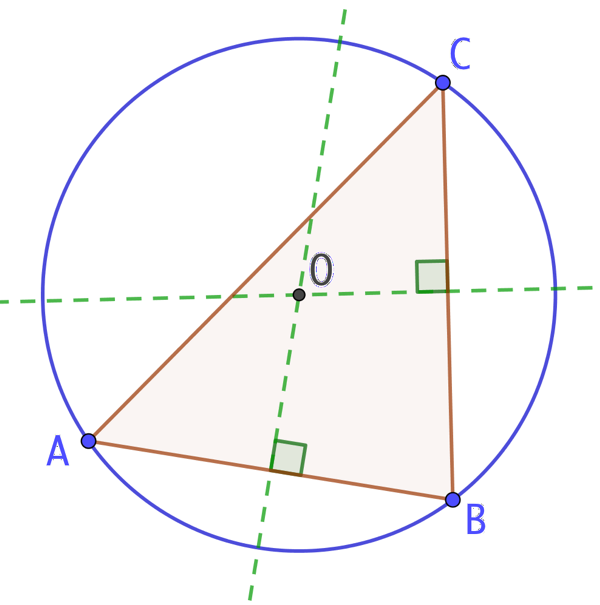 Dans l’exemple de droite, les médiatrices se coupent en O, centre du cercle passant par A, B et C, les trois sommets du triangle.
Dans l’exemple de droite, les médiatrices se coupent en O, centre du cercle passant par A, B et C, les trois sommets du triangle.
 Démonstration :
Démonstration :
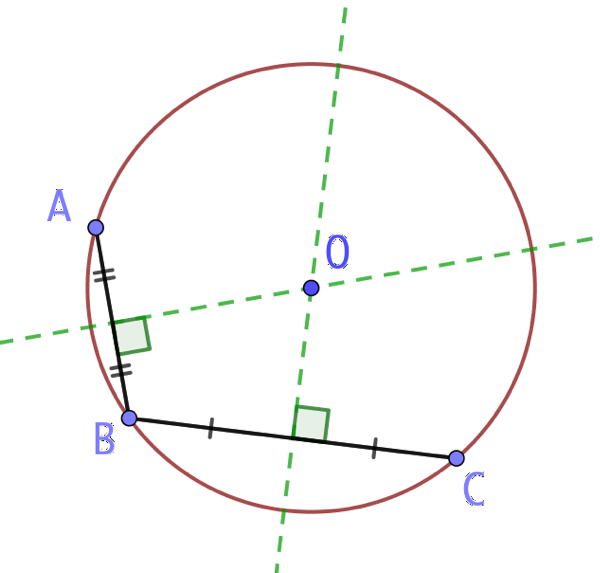
1ère partie (existence) : Soit A, B et C, trois points non alignés. Les médiatrices de [AB] et [BC] se coupent au point O. En considérant le triangle ABC, on déduit de la propriété précédente que ![]() , donc les points A, B et C appartiennent à un cercle de centre O et de rayon OA, qui est le cercle circonscrit à ABC.
, donc les points A, B et C appartiennent à un cercle de centre O et de rayon OA, qui est le cercle circonscrit à ABC.
2ème partie (unicité) : Supposons A, B et C appartiennent à un autre cercle de centre E. Alors ![]() . Donc E est équidistant des points A, B et C. Par conséquent, E appartient aux médiatrices de [AB] et [BC]. Donc E est le point d’intersection de ces deux médiatrices. On en conclut que E est confondu avec O, le centre du cercle circonscrit. Il y a donc un seul cercle passant par 3 points non alignés.
. Donc E est équidistant des points A, B et C. Par conséquent, E appartient aux médiatrices de [AB] et [BC]. Donc E est le point d’intersection de ces deux médiatrices. On en conclut que E est confondu avec O, le centre du cercle circonscrit. Il y a donc un seul cercle passant par 3 points non alignés.
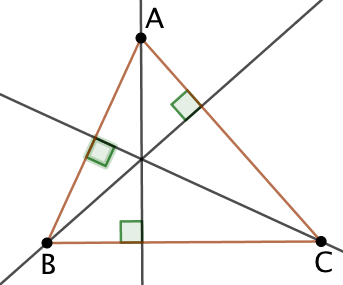
 Dans l’exemple de droite, la droite (AL) est la hauteur issue de A.
Dans l’exemple de droite, la droite (AL) est la hauteur issue de A.
Conséquence : Un triangle possède trois hauteurs. Dans le cas d’un triangle rectangle, deux de ses trois hauteurs sont confondues avec les deux côtés perpendiculaires du triangle.
 Pour lire la démonstration, cliquez ici.
Pour lire la démonstration, cliquez ici.
Remarque : Un triangle quelconque peut toujours être découpé en deux triangles rectangles. Il suffit pour cela d’abaisser l’une de ses hauteurs.
- Pour lire l’une des très nombreuses démonstrations de ce théorème, cliquez ici
- Pour lire la démonstration de la réciproque de ce théorème, cliquez ici.
Pour lire la démonstration, cliquez ici.
Démonstration : Les trois côtés d’un triangle équilatéral étant de même longueur, les trois angles sont de même mesure. Puisque la somme des trois vaut 180°, chaque angle mesure trois fois moins, soit 60°.
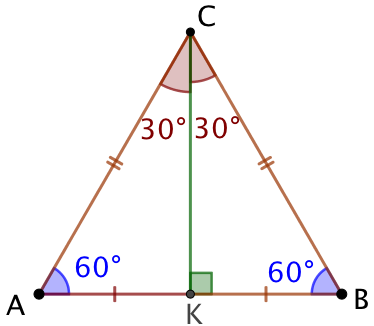 Démonstration : Soient le triangle équilatéral ABC et K le projeté orthogonal de A sur (BC). (AK) est la hauteur issue de A. Par ailleurs
Démonstration : Soient le triangle équilatéral ABC et K le projeté orthogonal de A sur (BC). (AK) est la hauteur issue de A. Par ailleurs ![]() donc A appartient à la médiatrice de [BC]. Comme la médiatrice est aussi perpendiculaire à (BC), il vient que la médiatrice et la hauteur sont parallèles. Comme elles ont en commun le point A, on en déduit qu’elle sont confondues.
donc A appartient à la médiatrice de [BC]. Comme la médiatrice est aussi perpendiculaire à (BC), il vient que la médiatrice et la hauteur sont parallèles. Comme elles ont en commun le point A, on en déduit qu’elle sont confondues.
Conséquence n°1: K, pied de la hauteur issue de A est aussi le milieu de [BC]. Comme le hauteur et la médiatrice sont confondues, que K appartient à la hauteur donc médiatrice, que la médiatrice coupe [BC] en son milieu, on en conclut que K est ce milieu.
Conséquence n°2: La hauteur (AK) découpe le triangle équilatéral ABC en deux triangles rectangles isométriques (superposables). K est le milieu de [AB] donc ![]() . ABC est équilatéral donc
. ABC est équilatéral donc ![]() . Par conséquent les deux triangles ACK et BCK, qui partage un troisième côté [CK] sont isométriques. Par construction, ils sont aussi rectangles.
. Par conséquent les deux triangles ACK et BCK, qui partage un troisième côté [CK] sont isométriques. Par construction, ils sont aussi rectangles.
IV – Trigonométrie dans le triangle rectangle
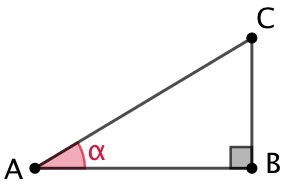 Étant donné un triangle ABC rectangle en B, on définit trois quantités liées à la mesure de l’angle
Étant donné un triangle ABC rectangle en B, on définit trois quantités liées à la mesure de l’angle ![]()
![]()
Démonstrations :
![]()
![]()
Le théorème de Pythagore appliqué au triangle ABC donne : ![]() , soit
, soit ![]()
![]()
 Démonstrations : On reprend la figure du triangle équilatéral découpé en deux triangles rectangles. Considérons que la longueur de chaque côté du triangle ABC est
Démonstrations : On reprend la figure du triangle équilatéral découpé en deux triangles rectangles. Considérons que la longueur de chaque côté du triangle ABC est ![]() .
.
K est le milieu de [AB] donc ![]() .
.
Dans le triangle rectangle AKC : ![]() .
.
Par ailleurs, ![]() , donc
, donc ![]() . Ce qui donne
. Ce qui donne ![]() .
.
On démontre de façon similaire que ![]() et qu’alors
et qu’alors ![]() .
.
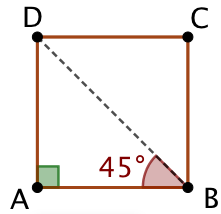 On considère à présent un carré ABCD de côté
On considère à présent un carré ABCD de côté ![]() . Une diagonale de ce carré le découpe en deux triangles rectangles et isocèles. Ainsi l’angle
. Une diagonale de ce carré le découpe en deux triangles rectangles et isocèles. Ainsi l’angle ![]() mesure 45°.
mesure 45°.
On démontre facilement en utilisant le théorème de Pythagore que ![]() .
.
![]() .
.
On démontre de façon similaire que ![]() .
.
V – Parallélogrammes
1) Définition et propriétés
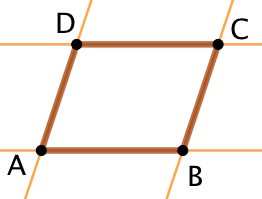 Exemple :
Exemple :
- Les droites (AB) et (CD) sont parallèles.
- Les droites (AD) et (BC) sont parallèles.
- Donc ABCD est un parallélogramme.
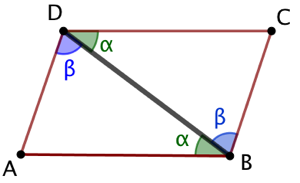 Démonstration : Soit le parallélogramme ABCD.
Démonstration : Soit le parallélogramme ABCD.
(AB) et (DC) sont parallèles donc les angles alternes-internes qu’elles forment avec (BD) sont de même mesure ![]() .
.
(AD) et (BC) sont parallèles donc les angles alternes-internes qu’elles forment avec (BD) sont de même mesure ![]() .
.
Par conséquent : les triangles ABC et CDB possédent un côté commun [BD] compris entre deux angles de même mesure; ils sont isométriques. Donc AB = DC et AD = NC.
Exemple : Soit le parallélogramme ABCD.
- On sait que les côtés opposés sont symétriques par rapport au milieu des diagonales. Donc ils ont la même longueur.
- On sait aussi qu’une symétrie centrale concerne les mesures d’angles. Donc les angles
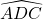 et
et 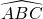 ont la même mesure, ainsi que les angles
ont la même mesure, ainsi que les angles 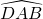 et
et 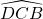 .
.
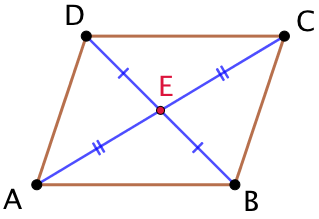 Exemple : Soit un parallélogramme ABCD.
Exemple : Soit un parallélogramme ABCD.
- Ses diagonales [AC] et [BD] se coupent en leur milieu E.
- E est le centre de symétrie de ABCD.
- [AB] et [CD] sont symétriques par rapport à E.
- [AD] et [BC] sont symétriques par rapport à E.
2) Savoir reconnaître un parallélogramme
Pour démontrer qu’un quadrilatère est un parallélogramme, on peut revenir à la définition du parallélogramme. Sinon, on peut utiliser l’une des propriétés suivantes sur les quadrilatères.
 Exemple : Soit ABCD un quadrilatère.
Exemple : Soit ABCD un quadrilatère.
Si on sait que les diagonales [AC] et [BD] de ce quadrilatère se coupent en leur milieu E, alors ABCD est un parallélogramme.
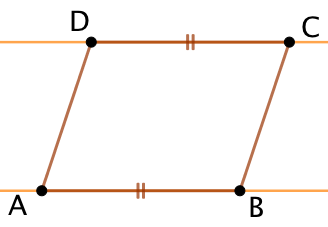 Exemple : Soit ABCD un quadrilatère.
Exemple : Soit ABCD un quadrilatère.
Si on sait que :
- les droites (AB) et (CD) sont parallèles ;
- les longueurs AB et CD sont égales ;
- les côtés [AB] et [CD] ne se croisent pas ;
Alors ABCD est un parallélogramme.
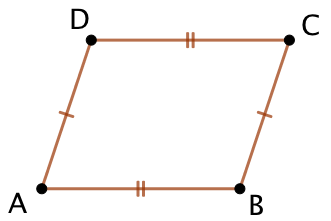 Exemple :
Exemple :
Soit ABCD un quadrilatère.
Si on sait que :
- les longueurs AB et CD sont égales ;
- les longueurs AD et BC sont égales ;
- les côtés [AB] et [CD] ne se croisent pas ;
Alors ABCD est un parallélogramme.
VI – Théorème de Thalès
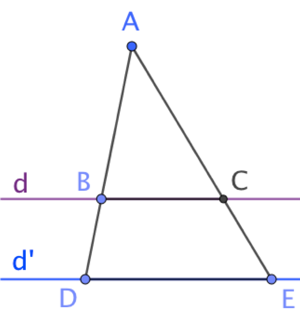 Étant donnés
Étant donnés
- un triangle ADE ;
- un point B sur le segment [AD] et
- un point C sur le segment [AE].
les droites ![]() et
et ![]() sont parallèles si et seulement si
sont parallèles si et seulement si ![]() .
.
Le théorème de Thales peut s’appliquer dans toute construction incluant deux droites parallèles et deux droites sécantes. Il établit des égalités de rapports entre certaines longueurs mesurées sur le triangle formé par la construction.
Pour lire la démonstration, cliquez ici.
Il s’agit d’un cas particulier du théorème de Thalès pour lequel les points B et C sont les milieux respectifs des segments [AD] et [AE].
Pour lire la démonstration, cliquer ici.
EXERCICES
- 64 / 165 : calcul de sinus et de longueur
- 67 / 166 : 2 cercles et 3 points alignés
- 68 / 166 : lunules
- 69 / 166 : 2 carrés et un cercle
- 71 / 166 : Varignon
- 79 / 168 : démontrer que le projeté d’un point est le point le plus proche de ce point
- 80 (partie A) / 168 : Pythagore et calculs algébriques
- 84 / 169 : médiatrices concourantes
- 85 / 169 : hauteurs concourantes
- 86 / 169 : calculs trigo
- 87 / 169 : Al-Kâshi
Exercice n°1 : Soit ABC un triangle rectangle en B. Soit D le milieu du du segment [AC]. Démontrer que les triangles ABD et BCD ont la même aire.
Exercice n°2 : Soit ABC un triangle rectangle en B. Soit H le projeté orthogonal de B sur (AC).
- Démontrer que pour tous réels
 et
et 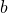 ,
, 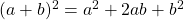 . Aide :
. Aide : 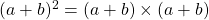 .
. - En utilisant le résultat précédent, démontrer que
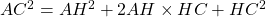 .
. - En utilisant le théorème de Pythagore dans les trois triangles rectangles de la figure, démontrer que
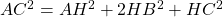
- En utilisant les deux résultats précédents, démontrer que
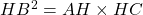 .
.
Exercice n°3 : Soient deux points A et B, et O le milieu du segment [AB]. On considère le cercle de centre O et de diamètre AB et un point C quelconque sur ce cercle. L’objectif est de démontrer que le triangle ABC est rectangle en C.
- Démontrer que pour tous réels
 et
et 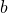 ,
, 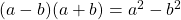 .
. - Expliquer pourquoi
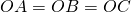 .
. - Soit H le projeté orthogonal de C sur (AB). En appliquant le théorème de Pythagore au triangle OHC et en utilisant la relation de la question a., démontrer que
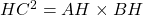 .
. - Écrire le théorème de Pythagore pour les triangles ACH et BCH.
- En utilisant les résultats des deux questions précédentes, démontrer que ABC est rectangle en C.
Exercice n°4 : L’objectif est de démontrer la réciproque de l’exercice précédent. Soit ABC un triangle rectangle en B. Soit H le projeté orthogonal de B sur (AC).
- En considérant le triangle rectangle OBH, en déduire une expression de
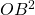 .
. - Sachant que
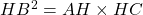 (résultat de l’exercice n°2), écrire autrement l’expression précédente.
(résultat de l’exercice n°2), écrire autrement l’expression précédente. - Exprimer AH et HC en fonction de AO et HO.
- En utilisant les résultats des deux questions précédentes, montrer que
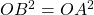 .
. - Conclure sur la nature du cercle de centre O et de diamètre AC.
Exercice n°5 : Soit un cercle pour lequel on cherche la position du centre.
- Soit deux points A et B du cercle. On trace deux droites perpendiculaires au segment [AB] et passant par A et par B. Ces deux droites coupent le cercle aux points C et D. Que peut on dire des triangles ABC et DBC ?
- En utilisant l’exercice précédent, en déduire la nature des segments [AC] et [BD] par rapport au cercle.
- Définissez alors la position du centre du cercle.
Exercice n°6 (n°67 page 166) : Soient deux cercles ![]() et
et ![]() de rayons différents sécants en A et B. Soit le point M de
de rayons différents sécants en A et B. Soit le point M de ![]() tel que AM soit un diamètre de
tel que AM soit un diamètre de ![]() et le point N de
et le point N de ![]() tel que AN soit un diamètre de
tel que AN soit un diamètre de ![]() . En utilisant le résultat de l’exercice n°3, démontrer que les points M, B et N sont alignés.
. En utilisant le résultat de l’exercice n°3, démontrer que les points M, B et N sont alignés.
Exercice n°7 : Soit ABC un triangle rectangle en A. Démontrer que l’aire du demi-disque de diamètre BC est égale à la somme des aires des demi-disques de diamètres respectifs AB et AC.
 Exercice n°8 (n°68 page 166) : Soit un triangle ABC rectangle en C. On trace trois demi-cercles de diamètre respectifs AB, AC et BC. On crée ainsi deux lunules (en bleu sur la figure). Démontrer que la somme des aires de ces deux lunules est égale à l’aire du triangle ABC.
Exercice n°8 (n°68 page 166) : Soit un triangle ABC rectangle en C. On trace trois demi-cercles de diamètre respectifs AB, AC et BC. On crée ainsi deux lunules (en bleu sur la figure). Démontrer que la somme des aires de ces deux lunules est égale à l’aire du triangle ABC.
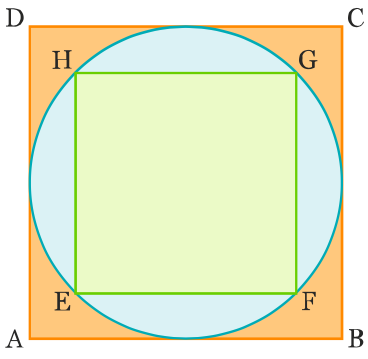 Exercice 9 (n°69 page 166) : On considère un carré EFGH inscrit dans un cercle C qui est lui-même inscrit dans un carré ABCD. Déterminer la proportion de la surface bleue par rapport à l’aire totale du carré ABCD.
Exercice 9 (n°69 page 166) : On considère un carré EFGH inscrit dans un cercle C qui est lui-même inscrit dans un carré ABCD. Déterminer la proportion de la surface bleue par rapport à l’aire totale du carré ABCD.
Exercice 10(n°86 page 169) : On considère un triangle JKL et on appelle H le projeté orthogonal de K sur la droite (JL).
- Donner la formule permettant de calculer l’aire du triangle JKL en utilisant les notations de l’énoncé.
- Démontrer que
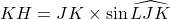 .
. - En déduire alors une nouvelle expression de l’aire du triangle JKL sans utiliser une hauteur.
- Calculer l’aire du triangle ABC telle que
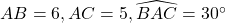 .
.
Exercice 11 – formule d’Al-Kâshi (n°87 page 169) : On considère un triangle quelconque ABC. On veut démontrer que : ![]() .
.
- Soit H le pied de la hauteur issue de B. Exprimer
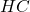 en fonction de
en fonction de 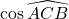 , puis
, puis 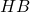 en fonction de
en fonction de 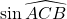 .
. - Exprimer
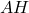 en fonction de
en fonction de 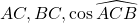
- Démontrer la formule d’Al-Kâshi.
Exercice 12 (n°84 page 169) : On considère un triangle ABC quelconque. On veut démontrer que les trois médiatrices dans le triangle ABC sont concourantes et que leur point d’intersection est le centre du cercle circonscrit au triangle. On appelle m1 la médiatrice du segment [AB], m2 la médiatrice du segment [AC] et m3 la médiatrice du segment [BC].
- Démontrer que m1 et m2 ne sont pas parallèles.
- On appelle O le point d’intersection de m1 et m2. Puisque O appartient à m1, quelle relation existe-t-il entre les longueurs OA et OB ?
- De même, comparer les longueurs OA et OC.
- Le point O appartient-il alors à m3 ?
- Quelle interprétation géométrique peut-on donner à la comparaison des trois longueurs OA,OB et OC ?
- Conclure en résumant les propriétés démontrées.
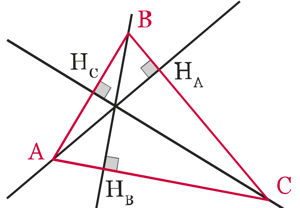 Exercice 13 (n°85 page 169) : On considère un triangle ABC quelconque avec ses trois hauteurs. HA, HB, et HC sont les pieds des hauteurs respectivement issues de A, B et C. On veut démontrer que les trois hauteurs sont concourantes.
Exercice 13 (n°85 page 169) : On considère un triangle ABC quelconque avec ses trois hauteurs. HA, HB, et HC sont les pieds des hauteurs respectivement issues de A, B et C. On veut démontrer que les trois hauteurs sont concourantes.
- Reproduire la figure et construire : la droite dA passant par A et parallèle à (BC), la droite dB passant par B et parallèle à (AC), la droite dC passant par C et parallèle à (AB), le point R, point d’intersection de dA et dB, le point S, point d’intersection de dB et dC, le point T, point d’intersection de dA et dC.
- Démontrer que les quadrilatères ABCT et ACBR sont des parallélogrammes.
- En déduire que A est le milieu de [RT].
- En déduire alors que la droite (AHA) est la médiatrice du segment [RT].
- De même, démontrer que (BHB) est la médiatrice de [RS] et que (CHC) est la médiatrice de [ST].
- En utilisant les médiatrices du triangle RST, que peut-on conclure sur les hauteurs du triangle ABC?
Exercice 14 : Un bâton de 1 m de longueur est posé verticalement sur le sol à une distance de 30 m d’une tour. L’ombre du bâton mesure 1,5 m. Quelle est la hauteur de la tour ?
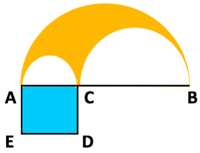 Exercice 15 : (figure de gauche) Les 3 points A, C, et B sont alignés. AB mesure 4 cm et le point C est mobile entre A et B. On trace trois cercles de diamètres respectifs AB, AC et CB. Existe-t-il une position de C telle que l’aire du carré bleu AEDC soit égale à l’aire jaune ?
Exercice 15 : (figure de gauche) Les 3 points A, C, et B sont alignés. AB mesure 4 cm et le point C est mobile entre A et B. On trace trois cercles de diamètres respectifs AB, AC et CB. Existe-t-il une position de C telle que l’aire du carré bleu AEDC soit égale à l’aire jaune ?
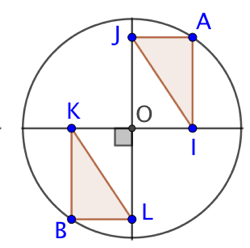 Exercice 16 : (figure de droite) Soient un cercle de centre O et deux diamètres perpendiculaires. OIAJ et OKBL sont deux rectangles. Quel est le plus long des deux segments [IJ] et [KL] ?
Exercice 16 : (figure de droite) Soient un cercle de centre O et deux diamètres perpendiculaires. OIAJ et OKBL sont deux rectangles. Quel est le plus long des deux segments [IJ] et [KL] ?
Exercice 17 : On considère un triangle ABC et on désigne par I,J et K les milieux respectifs des côtés [BC], [AC] et [AB]. L est le milieu de [JK] et D le milieu de [IK].
Prouver que les droites (LD) et (AB) sont parallèles.
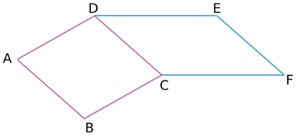 Exercice 18 : (figure de gauche) ABCD et CDEF sont des parallélogrammes. Démontrer que ABFE est un parallélogramme. En déduire que
Exercice 18 : (figure de gauche) ABCD et CDEF sont des parallélogrammes. Démontrer que ABFE est un parallélogramme. En déduire que ![]() .
.
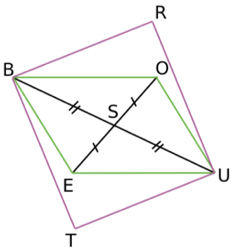 Exercice 19 : (figure de droite) BOUE et BRUT sont des parallélogrammes. Démontrer que TERO est un parallélogramme.
Exercice 19 : (figure de droite) BOUE et BRUT sont des parallélogrammes. Démontrer que TERO est un parallélogramme.
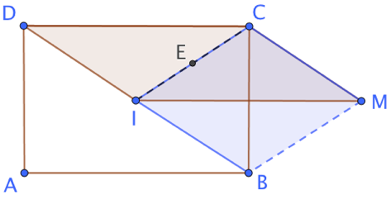 Exercice 20 : (figure de gauche) ABCD est un rectangle de centre I. E est le milieu de [IC]. M est le symétrique de D par rapport à E.
Exercice 20 : (figure de gauche) ABCD est un rectangle de centre I. E est le milieu de [IC]. M est le symétrique de D par rapport à E.
- Montrer que MIDC est un parallélogramme.
- En déduire la nature de MBIC.
Exercice 21 : Démontrer qu’un rectangle est un parallélogramme dont les diagonales sont de même longueur.
Exercice 22 : Une maison A est située à 10 m du bord rectiligne d’une route. Déterminer les points situés à 15 m de la maison et à 10 m du bord de la route.
Exercice 23 : EFG est un triangle rectangle en F tel que ![]() . Déterminer la valeur exacte de
. Déterminer la valeur exacte de ![]() puis son arrondi au centième.
puis son arrondi au centième.
 Exercice 24 : ABCD est un carré tel que AC = 10 cm. Calculer la longueur AB.
Exercice 24 : ABCD est un carré tel que AC = 10 cm. Calculer la longueur AB.
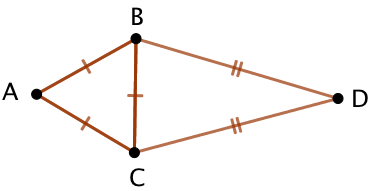
Exercice 25 : (figure de droite). ABC est un triangle équilatéral et BCD est un triangle isocèle en D. Les médiatrices de [AB] et [BD] se coupent en I et les médiatrices [AC] et [CD] se coupent en J.
- Construire une figure.
- Justifier que : IA = ID, JA = JD et IA = JA.
- En déduire la nature du quadrilatère AIDJ.
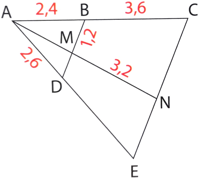 Exercice 26 : (figure de droite) Les droites (BC), (MN) et (DE) se coupent en A. Les points D, M, B d’une part et E, N, C d’autre part sont alignés. les droites (BD) et (CE) sont parallèles. Calculer les longueurs DE, AM et CN.
Exercice 26 : (figure de droite) Les droites (BC), (MN) et (DE) se coupent en A. Les points D, M, B d’une part et E, N, C d’autre part sont alignés. les droites (BD) et (CE) sont parallèles. Calculer les longueurs DE, AM et CN.
Exercice 27 : A est point situé à 3 cm d’une droite d.
- Construire et décrire l’ensemble des points situés à 3 cm de A.
- Construire et décrire l’ensemble des points situés à 3 cm de la droite d.
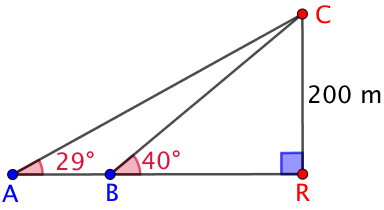 Exercice 28 : (figure de droite) Deux randonneurs A et B observent un chevreuil (point C).
Exercice 28 : (figure de droite) Deux randonneurs A et B observent un chevreuil (point C).
- À quelle distance, en m, du refuge se trouve le randonneur B ? Arrondir à l’unité.
- Quelle distance, en m, sépare les deux randonneurs ? Arrondir à l’unité.
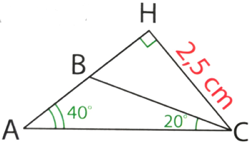 Exercice 29 : (figure de gauche) AHC est un triangle rectangle en H.
Exercice 29 : (figure de gauche) AHC est un triangle rectangle en H.
- Calculer la mesure de chacun des angles :
- Calculer chaque longueur, en cm. Arrondir au dixième : BH, BC et AC.
- Calculer l’aire, en cm2, du triangle ABC. Arrondir à l’unité.
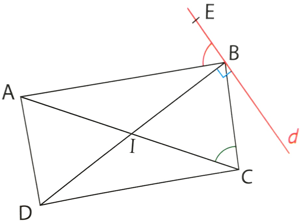 Exercice 30 : (figure de droite) ABCD est un rectangle de centre I. d est la droite perpendiculaire en B à (BD) et E est un point de d. Démontrer que
Exercice 30 : (figure de droite) ABCD est un rectangle de centre I. d est la droite perpendiculaire en B à (BD) et E est un point de d. Démontrer que ![]() .
.
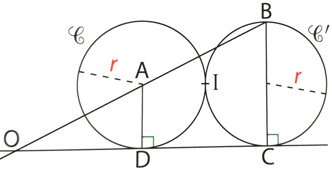 Exercice 31 : (figure de gauche). Exprimer la longueur OD en fonction de r.
Exercice 31 : (figure de gauche). Exprimer la longueur OD en fonction de r.
