Théorème de Pythagore

Un triangle ABC est rectangle en A si et seulement si AB² + AC² = BC².

Explications :

Il existe plusieurs centaines de démonstrations du théorème de Pythagore.

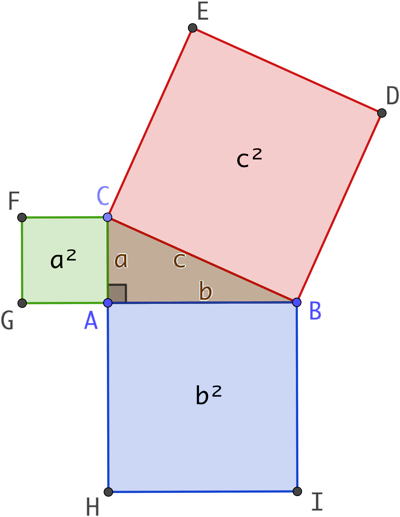
On pose a = AC, b = AB et c = BC

On remarque que a², b² et c² sont les aires des trois carrés construits à partir des trois côtés du triangle. Plusieurs démonstrations cherchent à prouver que l’aire du grand carré est égale à la somme des aires des deux autres carrés.

Démonstration de Garfield :

Abraham Garfield (1831-1881) qui fut le vingtième Président des Etats-Unis, a proposé l’une des démonstrations les plus simples. On ajoute au premier triangle ABC, un second triangle FDB égal à ABC. On va calculer de deux manières différentes l’aire du trapèze rectangle AFDC.

Le calcul direct : .

Le calcul par découpage : le trapèze est composé des triangles ABC, FDB et BDC.

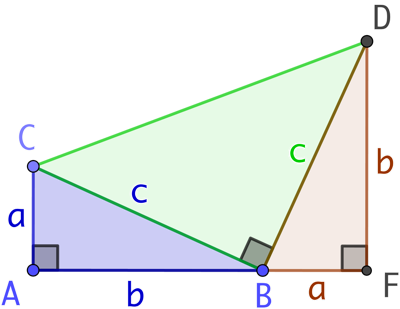L’aire de chacun des triangles ABC et FDB est .

L’aire du triangle BDC est . En effet BDC est un triangle rectangle en B. Pour s’en assurer, on remarque que : .

On écrit que les deux calculs donnent la même aire : .

Le calcul donne : .

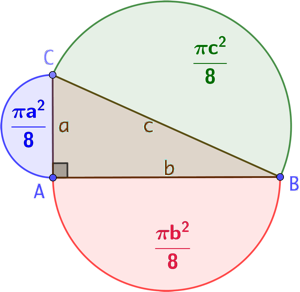Curiosité :

L’aire du demi-disque de diamètre c est la sommes des aires des demi-cercles de diamètre a et b.

Puisque ABC est un triangle rectangle en A, on sait que . Il suffit alors de multiplier les deux membres de cette égalité par pour obtenir :

.