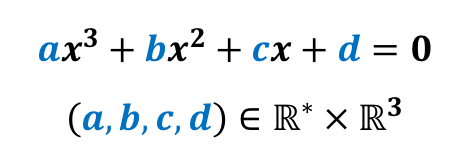On cherche les solutions de l’équation : ![]() sachant que
sachant que ![]() et
et ![]() sont des nombres complexes et que
sont des nombres complexes et que ![]() .
.
Méthode de Cardan
On se limite au cas où ![]() et
et ![]() sont des nombres réels.
sont des nombres réels.
On peut diviser par ![]() , ce qui donne
, ce qui donne ![]() .
.
On considère que ![]() est le début de l’identité remarquable
est le début de l’identité remarquable ![]() . On obtient alors :
. On obtient alors : ![]()
On veut faire apparaître une seconde fois l’expression ![]() :
: ![]()
Ce qui donne finalement : ![]()
L’équation à résoudre est : ![]() avec
avec ![]() et
et ![]()
Remarque : le terme en ![]() a disparu car la somme la somme des racines complexes de cette équation est nulle. À démontrer.
a disparu car la somme la somme des racines complexes de cette équation est nulle. À démontrer.
L’astuce consiste à remplacer la variable ![]() par deux variables
par deux variables ![]() et
et ![]() telles que
telles que ![]() . L’équation devient après développement et factorisation :
. L’équation devient après développement et factorisation : ![]() .
.
Comme on passe d’une à deux variables, on peut leur imposer une relation supplémentaire que l’on choisit afin de simplifier notre équation.
On impose que ![]() , ce qui donne
, ce qui donne ![]() donc
donc ![]() . Par ailleurs l’équation à résoudre se résume alors à
. Par ailleurs l’équation à résoudre se résume alors à ![]() .
.
Nous savons que deux nombres, dont on connait la somme ![]() et le produit
et le produit ![]() , sont les solutions de l’équation
, sont les solutions de l’équation ![]() .
.
Par conséquent ![]() et
et ![]() sont les solutions de l’équation
sont les solutions de l’équation ![]() .
.
![]() . Si
. Si ![]() alors on trouve
alors on trouve ![]() puis la solution réelle
puis la solution réelle ![]() de l’équation de départ. La quantité
de l’équation de départ. La quantité ![]() est appelée discriminant de l’équation
est appelée discriminant de l’équation ![]() .
.
Exemple (amusant) : ![]()
l’équation est déjà de la forme ![]() . En posant
. En posant ![]() , on obtient l’équation :
, on obtient l’équation : ![]()
La relation supplémentaire que nous imposons à ![]() et à
et à ![]() est :
est : ![]() , donc
, donc ![]() . L’équation devient alors :
. L’équation devient alors : ![]() .
.
Par conséquent ![]() et
et ![]() sont les solutions de l’équation
sont les solutions de l’équation ![]() . On trouve :
. On trouve : ![]() et
et ![]()
La solution réelle de l’équation ![]() est
est ![]() . Or il est assez simple de démontrer que cette solution est 1. Pour le prouver il suffit de calculer
. Or il est assez simple de démontrer que cette solution est 1. Pour le prouver il suffit de calculer ![]() et de constater que l’on retombe sur
et de constater que l’on retombe sur ![]() . La fonction cube étant strictement croissante, 1 est le seul nombre réel égal à son cube.
. La fonction cube étant strictement croissante, 1 est le seul nombre réel égal à son cube.
De cet exemple, on tire la consigne suivante : avant de se plonger dans la résolution laborieuse décrite dans cet article, il est conseillé de rechercher l’existence d’une solution évidente.
Propriété intermédiaire
L’équation ![]() admet une solution réelle unique si et seulement si
admet une solution réelle unique si et seulement si ![]() .
.
Pour cela on considère la fonction ![]() . Sa dérivée est
. Sa dérivée est ![]() .
.
Si ![]() alors la dérivée est positive et la fonction
alors la dérivée est positive et la fonction ![]() est croissante. Elle ne s’annule que pour une seule valeur de
est croissante. Elle ne s’annule que pour une seule valeur de ![]() , et bien entendu
, et bien entendu ![]() .
.
Si ![]() alors la dérivée est positive sur
alors la dérivée est positive sur ![]() et
et ![]() et négative sur
et négative sur ![]() .
.
Donc ![]() est croissante sur
est croissante sur ![]() et
et ![]() et décroissante sur
et décroissante sur ![]() .
.
Par conséquent ![]() admet un maximum relatif
admet un maximum relatif ![]() et un minimum relatif
et un minimum relatif ![]() . Pour que la fonction ne s’annule qu’une seule fois, il faut que
. Pour que la fonction ne s’annule qu’une seule fois, il faut que ![]() et
et ![]() soient de même signe, c’est à dire que
soient de même signe, c’est à dire que ![]() .
.
![]() . D’où le résultat.
. D’où le résultat.
Discriminant négatif
L’équation ![]() possède deux solutions complexes et conjuguées
possède deux solutions complexes et conjuguées ![]() . Les racines cubiques de
. Les racines cubiques de ![]() sont
sont ![]() . Pour chaque valeur, on trouve la racine cubique de
. Pour chaque valeur, on trouve la racine cubique de ![]() avec la relation supplémentaire :
avec la relation supplémentaire : ![]() , et par conséquent on détermine les 3 solutions de l’équation
, et par conséquent on détermine les 3 solutions de l’équation ![]() .
.
De plus, on démontre que ![]() :
:
![]() donc
donc ![]() avec
avec ![]() qui est un nombre réel. Donc
qui est un nombre réel. Donc ![]()
Par ailleurs ![]() . Par conséquent
. Par conséquent ![]() et
et ![]() . Ainsi
. Ainsi ![]()
Histoire : Cette méthode a été proposée par Jérôme Cardan dans son ouvrage Ars Magna publié en 1545. Cependant, Cardan se serait approprié la méthode en la volant à Niccolò Fontana dit Tartaglia (« Le Bègue »).