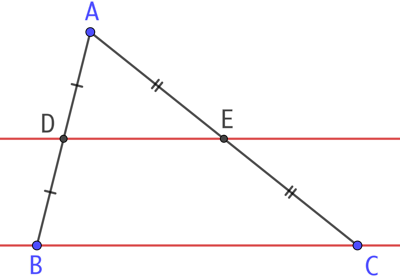
Étant donné un triangle quelconque, la droite reliant les milieux de deux côtés du triangle est parallèle à la droite portant le troisième côté. De plus la longueur du segment délimité par les deux milieux est la moitié de la longueur du troisième côté.
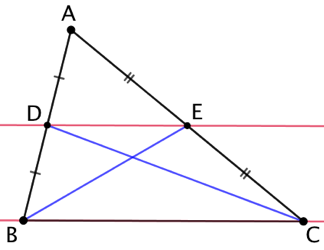
Première explication par les aires : On va démontrer que les triangles EDB et EDC ont la même aire.
Considérons le triangle ABE : comme D est le milieu de [AB], les triangles EDA et EDB ont la même aire.
Considérons le triangle ADC : comme E est le milieu de [AC], les triangles EDA et EDC ont la même aire.
Par conséquent les triangles EDB et EDC ont la même aire. Il vient alors que leurs sommets appartiennent à une droite (BC) parallèle à leur base commune [DE].
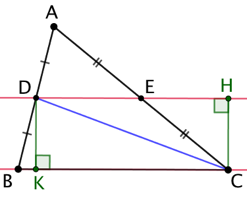Démontrer que BC = 2 x DE : Soit (CH) la hauteur de CED issue de C et (DK) la hauteur de DBC issue de D. (DE) et (BC) sont parallèles donc CH = DK. Par conséquent les aires de CED et DBC sont proportionnelles aux bases [BC] et [DE].
Or l’aire de CED est la moitié de celle de CAD car E est le milieu de [AC]. Par ailleurs l’aire de CDA est égale à l’aire de DBC car D est le milieu de [AB].
Conclusion : l’aire de CED est la moitié de celle de DBC. Comme ces aires sont proportionnelles aux bases des triangles, il vient que BC = 2 x DE.
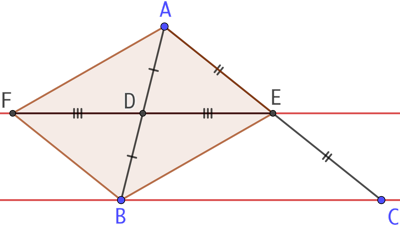Deuxième explication : On démontre ce théorème en utilisant des propriétés des parallélogrammes. L’idée est de montrer que les droites (DE) et (BC) portent deux côtés opposés, donc parallèles, d’un parallélogramme. On va construire deux parallélogrammes particuliers qui vont nous permettre d’utiliser le fait que D et E sont les milieux des côtés AB et AC.
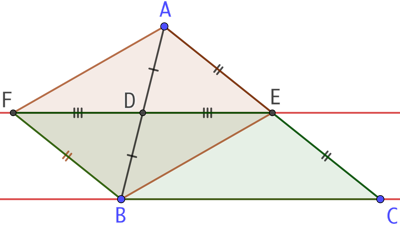
Soit F le symétrique de E par rapport à D. Alors D est par construction le milieu de [EF].
Mais D est aussi par hypothèse le milieu de [AB]. Par conséquent les deux diagonales du quadrilatère AFBE se coupent en leur milieu. On en conclut que AFBE est un parallélogramme.
Si AFBE est un parallélogramme alors ses côtés opposés sont parallèles et de même longueur. Donc (FB) et (AE) sont parallèles et FB = AE.
Or par hypothèse E est le milieu de [AC] donc AE = EC. Mais puisque FB = AE, on peut affirmer que FB = EC.
Par ailleurs les points A, E et C sont par hypothèse alignés. SI (FB) et (AE) sont parallèles alors (FB) et (EC) sont parallèles.
Nous venons de montrer que (FB) et (EC) sont parallèles et que les longueurs FB et EC sont égales : on en conclut que le quadrilatère FBCE est un parallélogramme et qu’alors les droites (FE) et (BC) sont parallèles, c’est-à-dire que les droites (DE) et (BC) sont parallèles.
Puisque D est le milieu de [FD], FD = DE, c’est-à-dire : FE = 2 x DE. Comme FBCE est un parallélogramme, FE = BC. Conclusion : BC = 2 x DE.
Réciproque du théorème de la droite des milieux : Étant donné un triangle quelconque ABC et D le milieu du segment [AB], la droite passant par D et parallèle à (BC) coupe le côté AC en son milieu.
Pour démontrer que E est le milieu de [AC], on va montrer que les aires des triangles ABE et EBC sont égales.
Les aires des triangles ADC et DBC sont égales à la moitié de celle de ABC car D est le milieu de [AB].
Les aires des triangles DBC et EBC sont égales car leurs sommets D et E sont placés sur une droite parallèle (DE) à leur base (BC). Par conséquent l’aire de EBC est égale à la moitié de l’aire de ABC. Ce qui impose que l’aire de ABE est aussi égale à la moitié de ABC.
Étant donné que les aires de ABE et EBC sont égales à la moitié de celle de ABC, il vient que E est le milieu de [AC].
Remarque : le théorème des milieux n’est qu’un cas particulier du théorème de Thalès.
