Théorème de Thales


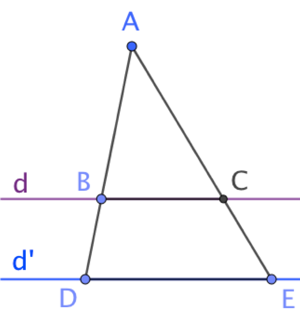
Le théorème de Thales peut s’appliquer dans toute construction incluant deux droites parallèles et deux droites sécantes. Il établit des égalités de rapports entre certaines longueurs mesurées sur le triangle formé par la construction.

Le théorème : Étant donnés

  • un triangle ADE ;
  • un point B sur le segment [AD] et
  • un point C sur le segment [AE].

Si les droites (BC) et (DE) sont parallèles, alors : \dfrac{AB}{AD} = \dfrac{AC}{AE} = \dfrac{BC}{DE}

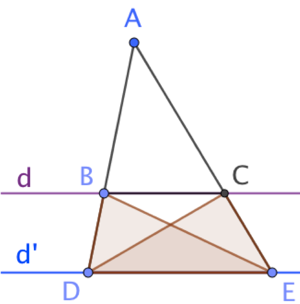Explications : L’idée est d’établir des égalités d’aires de triangles choisis de telle manière que ces aires soient proportionnelles à des longueurs.

Première partie : Dans cette partie on va démontrer que \dfrac{AB}{AD} = \dfrac{AC}{AE}

Les triangles DEB et DEC ont la même base et leurs sommets sont situés sur une droite parallèle à leur base, ils ont donc la même aire : A_{DEB} = A_{DEC}

On observe que A_{ABE} = A_{ADE} - A_{DEB} et A_{ADC} = A_{ADE} - A_{DEC}.
Puisque A_{DEB} = A_{DEC} alors A_{ABE} = A_{ADC}.
On peut donc écrire l’égalité : \dfrac{A_{DEB}}{A_{ABE}} = \dfrac{A_{DEC}}{A_{ADC}}.

Les triangles DEB et ABE ont un sommet commun E et leur base est située sur la même droite (AD). Donc leur surface est proportionnelle à leur base. Alors : \dfrac{A_{DEB}}{A_{ABE}} = \dfrac{BD}{AB}. Par un raisonnement identique, on établit que \dfrac{A_{DEC}}{A_{ADC}} = \dfrac{CE}{AC}.

Ce qui permet d’écrire que \dfrac{BD}{AB} = \dfrac{CE}{AC}, donc \dfrac{BD}{CE} = \dfrac{AB}{AC} = \dfrac{BD + AB}{CE + AC} = \dfrac{AD}{AE}. On en conclut que \dfrac{AB}{AD} = \dfrac{AC}{AE}.


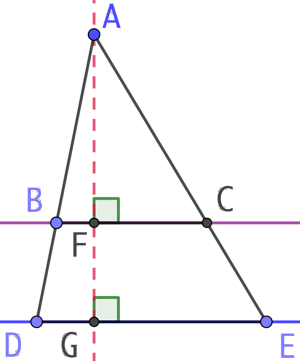
Seconde partie : On va démontrer que \dfrac{BC}{DE} = \dfrac{AB}{AD}

On trace la hauteur de ABC issue de A. Elle coupe (BC) en F et (DE) en G.

Les triangles CFG et CFE ont une base en commun [CF] et deux sommets G et E situés sur la droite (GE) parallèle à (BC). Donc A_{CFG} = A_{CFE}. En ajoutant à chaque membre de l’égalité A_{AFC}, on obtient A_{CFG} + A_{AFC}= A_{CFE} + A_{AFC}, soit A_{AGC} = A_{AFE}.

A_{AGC} = \dfrac{AG \times CF}{2} puisque CF est la hauteur du triangle AGC issue de C.
A_{AFE} = \dfrac{AF \times EG}{2} puisque EG est la hauteur du triangle AFE issue de E.

Comme A_{AGC} = A_{AFE}, il vient \dfrac{AG \times CF}{2} = \dfrac{AF \times EG}{2}, soit AG \times CF = AF \times EG, c’est à dire \dfrac{AF}{AG} = \dfrac{CF}{EG}.

On démontre de la même manière que \dfrac{AF}{AG} = \dfrac{BF}{DG}. On en déduit que : \dfrac{AF}{AG} = \dfrac{CF}{EG} = \dfrac{BF}{DG} = \dfrac{CF+BF}{EG+DG} = \dfrac{BC}{DE}.

En appliquant l’égalité démontrée dans la première partie au triangle AGE, il vient : \dfrac{AF}{AG} = \dfrac{AC}{AE}.

En appliquant l’égalité démontrée dans la première partie au triangle ADG, il vient : \dfrac{AF}{AG} = \dfrac{AB}{AD}.

Comme on vient de démontrer que \dfrac{AF}{AG} = \dfrac{BC}{DE}, on peut conclure la démonstration : \dfrac{BC}{DE} = \dfrac{AB}{AD} = \dfrac{AC}{AE}.

Remarque : Il s’agit des propositions VI.2, VI.3, VI.4 des Éléments d’Euclide.

Print Friendly, PDF & Email