Étant donné un triangle équilatéral de côté c, comment construire un carré de périmètre égal à celui du triangle ?.
L’idée : le périmètre du triangle est 3c. Donc la longueur d’un côté du carré est 3c/4. Il faut donc construire un segment de longueur 3c/4. On va utiliser deux fois le théorème des milieux.
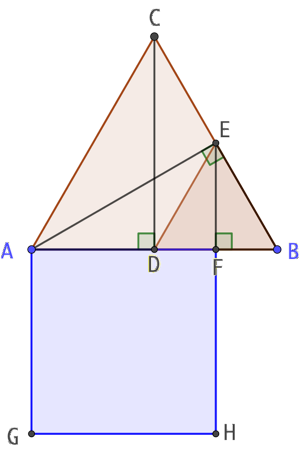
Construction :
- On trace le triangle équilatéral ABC de côté c;
- On trace la médiatrice du segment [AB]. ABC étant équilatéral donc isocèle en C, cette médiatrice passe par C;
- On trace la médiatrice issue de [BC]. ABC étant équilatéral donc isocèle en A, cette médiatrice passe par A;
- On trace le segment [DE];
- On considère le triangle DBE. On trace la médiatrice de [DB]. DBE étant équilatéral donc isocèle en E, cette médiatrice passe par E;
- Alors AF = 3c/4.
- On peut alors construire le carré AGHF de côté 3c/4.
Explications :
(CD) est la médiatrice de [AB] donc D est le milieu de [AB] et par conséquent DB = c/2. (AE) est la médiatrice de [BC] donc E est le milieu de [BC] et par conséquent EB = c/2. Par application du théorème des milieux au triangle ABC, on en conclut que DE = AC / 2 = c/2. Ce qui permet d’affirmer que DBE est un triangle équilatéral.
(EF) est la médiatrice de [DB] donc F est le milieu de [DB] et par conséquent FB = c/4. Donc AF = AD + DF = c/2 + c/4 = 3c/4.
