Soient deux points A et B. La médiatrice du segment [AB] se construit ainsi :
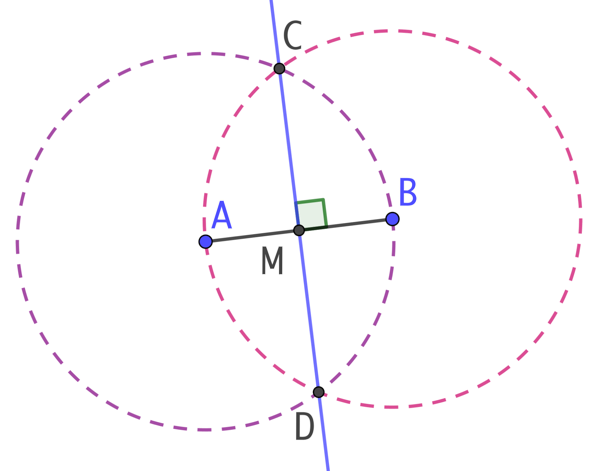
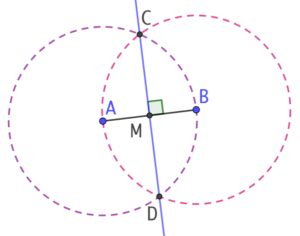
- On trace le segment [AB].
- On trace deux cercles de même rayon, de centre A et B. Ces deux cerclent se croisent en deux points C et D. Pour éviter toute mesure ou modification involontaire de l’écartement du compas, il suffit de tracer le cercle de centre A passant par B et le cercle de centre B passant par A.
- On trace la droite (CD). C’est la médiatrice de [AB]. Cela nous donne également la position du point M, milieu de [AB]. On observe que (CD) est perpendiculaire à (AB).
Explications :
Le point C se situe sur les deux cercles de centre A et B et dont le rayon est le même. Par conséquent les longueurs CA et CB sont égales. Pour les mêmes raisons on a DA = DB.
Or la médiatrice d’un segment est le lieu de tous les points équidistants (à même distance) des deux extrémités du segment. Par conséquent C et D appartiennent à la médiatrice de [AB]. La médiatrice, dont on sait que c’est une droite, est la droite (CD).
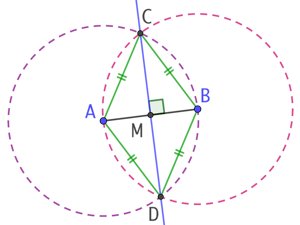
On remarque que l’on a ainsi construit le losange ACBD et que l’on vérifie que ces deux diagonales se coupent en leur milieu et sont perpendiculaires.
