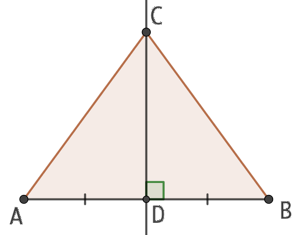
 La médiatrice d’un segment est le lieu des points équidistants des deux extrémités des segments.
La médiatrice d’un segment est le lieu des points équidistants des deux extrémités des segments.
Explications :
La médiatrice du segment [AB] est la droite perpendiculaire à (AB) et passant par le milieu D de [AB].
Soit D un point de cette médiatrice. La droite de (CD) est donc cette médiatrice et les triangles CAD et CDB sont rectangle en D.
Donc ![]() et
et ![]() . Comme D est le milieu de [AB], il vient que
. Comme D est le milieu de [AB], il vient que ![]() . Donc
. Donc ![]() , soit
, soit ![]() ce qui achève de démontrer que C est équidistant des points A et B.
ce qui achève de démontrer que C est équidistant des points A et B.
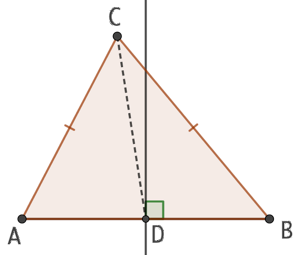 Réciproque : Si un point C est équidistant de A et de B alors il appartient à la médiatrice du segment [AB].
Réciproque : Si un point C est équidistant de A et de B alors il appartient à la médiatrice du segment [AB].
Supposons que C n’appartient pas à la médiatrice de [AB] et soit D le milieu de [AB]. Compte tenu de toutes ces hypothèses, les triangles CAD et CDB sont isométriques. Ainsi ![]() ce qui n’est manifestement pas le cas.
ce qui n’est manifestement pas le cas.
Donc C appartient à la médiatrice de [AB].
