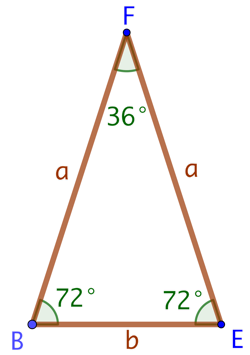
 Un triangle d’or est un triangle isocèle dont les deux côtés de même longueur mesurent
Un triangle d’or est un triangle isocèle dont les deux côtés de même longueur mesurent ![]() et le troisième côté mesure
et le troisième côté mesure ![]() tels que
tels que ![]() , le nombre d’or.
, le nombre d’or.
On démontre que les angles d’un triangle d’or mesurent 72°, 72° et 36°.
Explications :
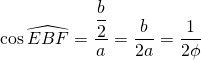 .
.
Or nous savons que ![]() (Voir cosinus de 36°) et que
(Voir cosinus de 36°) et que ![]() .
.
Donc ![]() .
.
On peut en conclure que ![]() mesure 72° et que
mesure 72° et que ![]() .
.
Remarque :
![]() .
.
