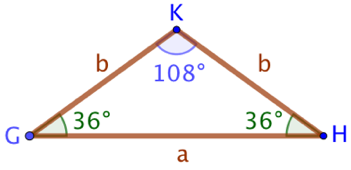
Un triangle d’argent est un triangle isocèle dont les deux côtés de même longueur mesurent 
et le troisième côté mesure 
tels que 
, le nombre d’or.
On démontre que les angles d’un triangle d’argent mesurent 36°, 36° et 108°.
Explications :
.
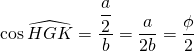Or nous savons que 
(Voir cosinus de 36°).
On peut en conclure que 
mesure 36° et que 
.
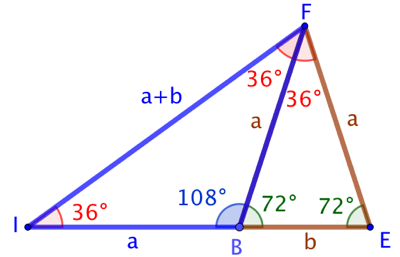Curiosité : On peut toujours former un triangle d’or à partir d’un triangle d’or et d’un triangle d’argent.
Le triangle FIE est un triangle d’or composé d’un autre triangle d’or FBE et d’un triangle d’argent FIB.
Explications :
Il faut vérifier que les dimensions de FIE respectent le coefficient de proportion 
, le nombre d’or. C’est-à-dire, a-t-on l’égalité : 
? On va utiliser le fait que 
.
.
