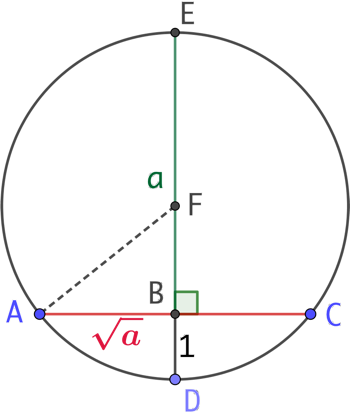
 On construit la racine carrée du nombre a en reprenant le protocole de construction du carré du nombre a :
On construit la racine carrée du nombre a en reprenant le protocole de construction du carré du nombre a :
- On trace un segment BE de longueur a.
- On le prolonge par un segment BD de longueur 1.
- On place le point F milieu du segment [ED].
- On trace le cercle de centre F passant par E,
- On trace la perpendiculaire à ED passant par B. Cette perpendiculaire coupe le cercle en deux points A et C. La longueur du segment [AB] vaut
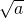 .
.
Explications :
![]()
![]()
On considère le triangle BAF rectangle en B. Selon Pythagore, ![]() .
.
Donc ![]() .
.
Conclusion : ![]() .
.
Remarque : AB est la moyenne géométrique de BD et BE.
Remarque : Il s’agit de la proposition VI.13 des Éléments d’Euclide.
