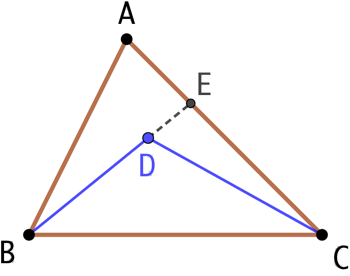
Étant donné un triangle ABC et un point D à l’intérieur de ce triangle, 
et AB + AC > DB +DC.
Explications :
est un angle extérieur au triangle DEC donc 
.
De même 
est un angle extérieur au triangle BAE donc 
.
Comme 
, on peut donc en conclure que .
En appliquant l’inégalité triangulaire au triangle BAE, on obtient BA + AE > BE, donc BA + AE + EC > BE + EC, soit BA +AC > BE + EC.
De la même façon, à partir du triangle DEC, on obtient DE + EC > DC, donc DE + EC + BD > DC + BD, soit BE + EC > DC + BD.
Conclusion : BA + AC > BD + DC
Remarque : Il s’agit de la proposition n°I.21 des Éléments d’Euclide.
