On construit un segment dont la longueur vaut le tiers de celle d’un segment [AB] ainsi :
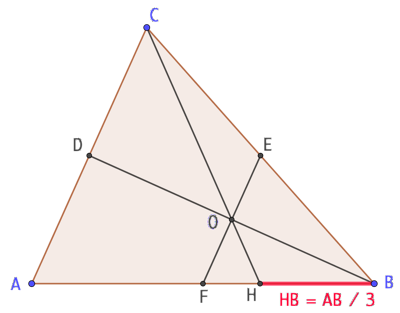
- On place un point C quelconque n’appartenant pas à la droite (AB) et on trace le triangle ABC.
- On place les points D, E et F, milieux respectifs des segments [AC], [CB] et [BA].
- On trace les segments [DB] et [EF]. Ils se coupent au point O.
- On trace la demi-droite [CO). Elle coupe le segment [AB] au point H. La longueur HB est égale au tiers de la longueur AB.
 Explications :
Explications :
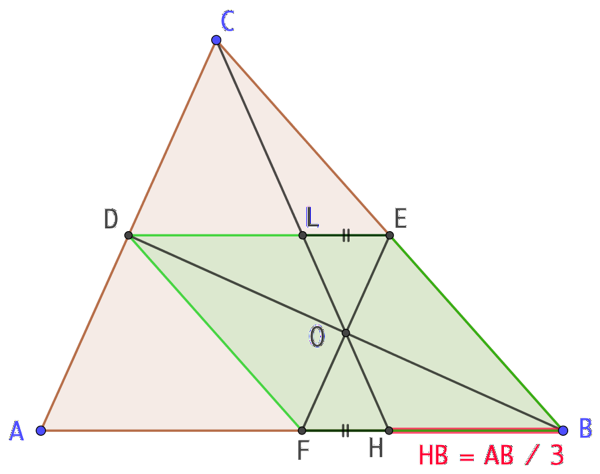
On utilise le théorème des milieux. D et E sont les milieux respectifs de [AC] et [CB], donc (DE) est parallèle à (AB). Autrement dit (DE) et (FB) sont parallèles.
De même, D et F sont les milieux respectifs de [AC] et [AB], donc (DF) est parallèle à (CB). Autrement dit (DF) et (EB) sont parallèles.
On peut alors affirmer que DFBE est un parallélogramme. Dans cas le point O est l’intersection des diagonales de DFBE, donc le centre de symétrie de DFBE.
Soit L le point d’intersection des segments [DE] et [CH]. Le théorème de Thalès nous permet d’écrire que HB = 2 x LE. Par la symétrie de centre O, on a l’égalité des distances : LE = FH. Par conséquent HB = 2 x FH ou FH = 0,5 x HB
FB = FH + HB = 0,5 x HB + HB = 1,5 x HB. Or FB = 0,5 x AB.
Donc 0,5 x AB = 1,5 x HB. Ce qui permet de conclure que HB = AB / 3.
