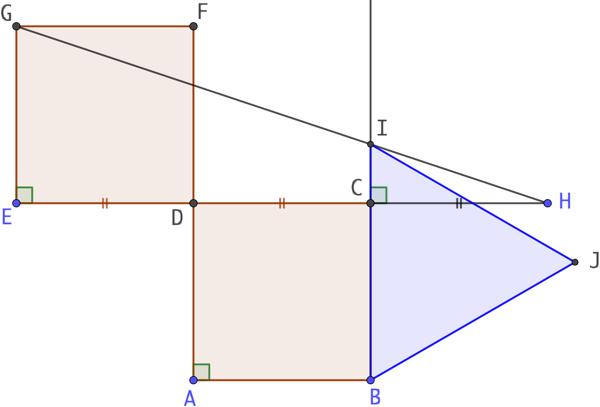
Étant donné un carré de côté c, comment construire un triangle équilatéral de périmètre égal à celui du carré ?.
L’idée : le périmètre du carré est 4c. Donc la longueur d’un côté du triangle équilatéral est 4c/3. Il faut donc construire un segment de longueur 4c/3. Qui dit fraction dit parfois théorème de Thales.
Construction :
- On trace le carré ABCD de côté c;
- On place le point E symétrique de C par rapport à D;
- On ajoute le carré EDFG de côté c;
- On place le point H symétrique de D par rapport à C;
- On trace le segment [GH];
- On trace la droite (BC). Celle-ci coupe [GH] en I;
Par construction, les droites (EG) et (CI) sont perpendiculaires à (EH). Donc (EG) // (CI). On peut alors utiliser le théorème de Thales dans le triangle EGH. Ainsi CI / EG = CH / EH. Or par construction EH = 3 x CH. Donc CI / EG = 1/3 c’est-à-dire CI = EG / 3.
Comme EG = BC = c , on en déduit que CI = c/3 et que BI = BC + CI = c + c/3 = 4c/3. On a donc construit un segment [BI] de longueur 4c/3. Il ne reste plus qu’à construire le triangle équilatéral BJI dont le périmètre mesure 4c.