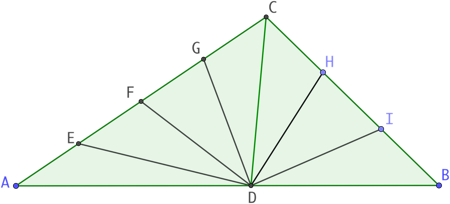
On souhaite diviser un triangle ABC quelconque pour obtenir sept triangles de même aire. On sait que AC mesure 40 cm et BC mesure 30 cm. Comment construire la figure et où se situe le point D ?
Explications :
Les quatre triangles rouges ont tous la même hauteur [DJ]. Donc leur aire est proportionnelle à leur base, le côté opposé au sommet D. Pour qu’ils aient la même il faut que leur base ait la même longueur : AE = EF = FG = GC = AC / 4 = 10 cm.
Les trois triangles verts ont tous la même hauteur [DK]. Pour qu’ils aient la même il faut que leur base ait la même longueur : BI = IH = HC = BC / 3 = 10 cm.
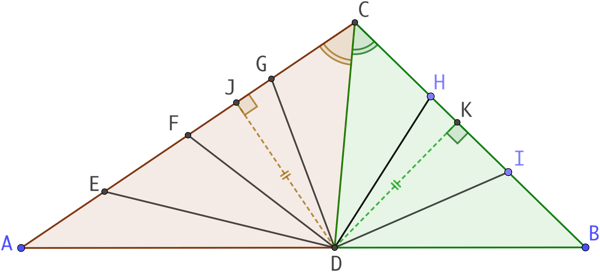
Pour que le triangle rouge CDG et le triangle vert CDH aient la même aire, sachant que leur base mesure 10 cm, il convient que leur hauteur ait la la même longueur : DJ = DK. Cette condition sera remplie si D appartient à la médiatrice de l’angle ACB.
Or la bissectrice (AD) découpe le segment [AB] en deux parties dans le rapport de ses côtés adjacents : DA / DB = CA / CB = 4/3. Donc AB / AD = (AD + DB) / AD = 1 + DB / AD = 1 + 3/4 = 7/4. Donc AD / AB = 4/7
