On veut démontrer que si ABC est un triangle rectangle en A alors 
.
Explications :
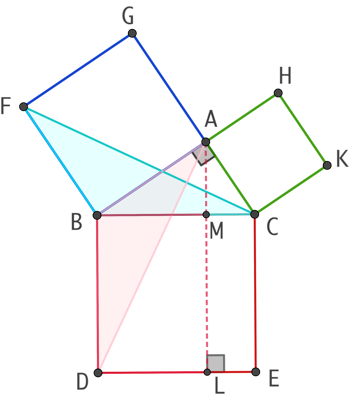
Les triangles FBC et ABD sont isométriques car ils ont deux côtés de même longueur délimitant un angle de même mesure :
- FB = BA (FBAG est un carré).
- BC = BD (BDEC est un carré).
.
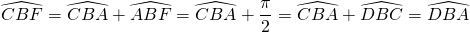La base [FB] du triangle FBC est l’un des côté du carré FBAG et le sommet C de FBC appartient à la droite (GA). Par conséquence l’aire de FBAG est le double de celle de FBC.
Pour des raisons similaires, l’aire du carré rectangle BDLM est le double de celle du triangle ABD.
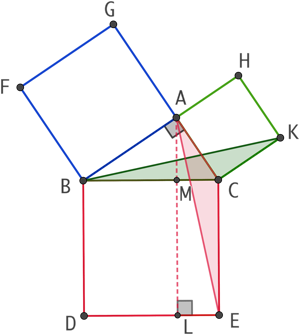Mais étant donné qu’il a été démontré que les triangles FBC et ABD sont isométriques, donc de même aire, il vient que les quadrilatères FBAG et BDLM ont la même aire.
C’est-à-dire : 
. (1)
Un même raisonnement permettrait de démontrer que les triangles BCK et AEC ont la même aire et que par conséquent les quadrilatères ACKH et MLEC ont la même aire.
C’est-à-dire : 
. (2)
En addition (1) et (2), il vient :
.
Remarque : Il s’agit de la proposition I.47 des Éléments d’Euclide.
Remarque : On peut consulter la démonstration plus simple du Président Garfield.
