Symétrie orthogonale d’une droite à la règle seule

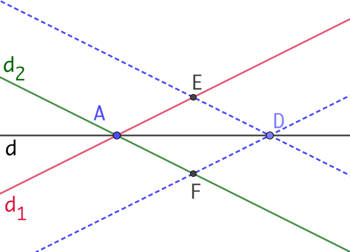
Étant donné une droite d, on construit ainsi la symétrie orthogonale d’une droite sécante d₁ par rapport à d :

• On place la règle sur la droite d₁ et on trace une droite le long de l’autre bord de la règle. Cette droite coupe d au point D.
• On fait pivoter la règle pour que A soit positionné sur l’autre bord de la règle et qu’il en soit de même pour D. On trace deux droites le long des bords de la règle, dont d₂ qui passe par A et qui est la symétrie orthogonale de d₁ par rapport à d.

Explications :

On sait (voir Milieu et médiatrice d’un segment à la règle seule) que ce programme de construction permet d’obtenir le losange AFDE. (AD) est l’une des deux diagonales qui est un axe de symétrie des deux côtés consécutifs [AE] et [AF]. Ce qui permet d’affirmer que d₁ et d₂ sont symétriques par rapport à d.