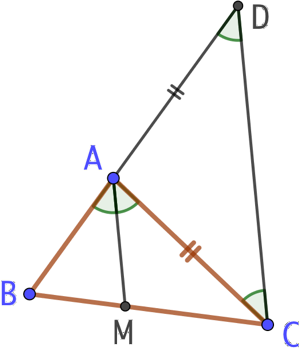
Étant donné un triangle ABC. La bissectrice (AM) découpe (BC) dans le rapport de ses côtés adjacents [AB] et [AC]. C’est-à-dire que 
.
Explications :
On complète la figure avec la parallèle à (AM) passant par C. Elle coupe (BA) au point D. Comme (AM) et (DC) sont parallèles, on en déduit les égalités de mesures d’angles :
et 
.
Or (AM) est la bissectrice de l’angle 
donc 
.
On en conclut que 
et que le triangle DAC est isocèle en A, soit AD=AC.
Le théorème de Thales appliqué au triangle BDC permet d’écrire l’égalité 
, soit .
Voir la réciproque : Condition pour une bissectrice
