Soient ABC un triangle et M un point du segment [BC]. 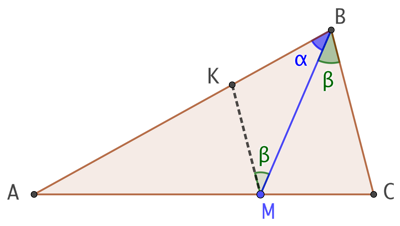 La droite (BM) est la bissectrice intérieure de l’angle
La droite (BM) est la bissectrice intérieure de l’angle ![]() si
si ![]() .
.
Explications :
On trace la droite (KM) parallèle à (BC) afin de pouvoir utiliser le théorème de Thales et démontrer que ![]() .
.
On observe que ![]() .
.
![]() .
.
![]() donc
donc ![]() .
.
Donc ![]() , soit
, soit ![]() .
.
Ainsi le triangle KMB est isocèle en B. Ce qui permet de conclure que ![]() .
.
(BM) est bien la médiatrice intérieure de ![]() .
.
Voir la réciproque : Sécante découpée par une bissectrice
