I – Définitions et propriétés
Autrement dit :![]() .
.
Exemple : ![]() car
car ![]() .
.
ATTENTION : ![]() n’a aucun sens car un nombre réel négatif n’a pas de racine carrée.
n’a aucun sens car un nombre réel négatif n’a pas de racine carrée.
Démonstration par l’absurde : supposons que ![]() . D’après la définition de la racine carrée, cela signifie que
. D’après la définition de la racine carrée, cela signifie que ![]() . Or, nous savons d’après la règle des signes que le produit d’un nombre par lui-même est toujours positif. Donc il n’existe pas de nombre dont le carré soit négatif. Notre supposition de départ était fausse.
. Or, nous savons d’après la règle des signes que le produit d’un nombre par lui-même est toujours positif. Donc il n’existe pas de nombre dont le carré soit négatif. Notre supposition de départ était fausse.
- Si
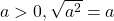
- Si
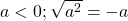
Démonstration : Soit ![]() . Par définition de la racine carré d’un nombre positif,
. Par définition de la racine carré d’un nombre positif, ![]() .
.
1er cas : ![]() , donc
, donc ![]() .
.
Alors ![]()
2ème cas : ![]() , donc
, donc ![]() . On sait que
. On sait que ![]() donc on peut calculer la racine carrée de
donc on peut calculer la racine carrée de ![]() .
.
Alors ![]()
Démonstration :
1ère partie : Supposons que deux nombres ![]() et
et ![]() ont le même carré :
ont le même carré : ![]() alors
alors ![]() .
.
On rappelle l’identité remarquable : ![]() .
.
Donc nous avons à résoudre l’équation : ![]() . Un produit de facteurs est nul si l’un au moins des facteurs est nul.
. Un produit de facteurs est nul si l’un au moins des facteurs est nul.
Ce qui nous amène à ![]() ou
ou ![]() , c’est-à-dire :
, c’est-à-dire : ![]() ou
ou ![]() .
.
2ème partie :
Si ![]() , alors
, alors ![]() .
.
Si ![]() alors
alors ![]() .
.
Démonstration : on va commencer par démontrer que ![]() et
et ![]() ont le même carré.
ont le même carré.
![]() car c’est la définition de la racine carrée.
car c’est la définition de la racine carrée.
![]() .
.
Puisque ![]() et
et ![]() ont le même carré et que
ont le même carré et que ![]() et
et ![]() sont tous les deux positifs, c’est qu’ils sont égaux d’après la propriété précédente.
sont tous les deux positifs, c’est qu’ils sont égaux d’après la propriété précédente.
Démonstration : il suffit de se rappeler que ![]() puis on applique la propriété précédente.
puis on applique la propriété précédente.
Démonstration : On va calculer les carrés des deux termes de l’inégalité :
![]() , c’est la définition de la racine carrée.
, c’est la définition de la racine carrée.
Pour calculer ![]() , on utilise l’identité remarquable =
, on utilise l’identité remarquable = ![]()
![]()
Ce qui donne : ![]() .
.
Par conséquent ![]() .
.
Comme la fonction carrée est croissante sur ![]() , on peut en conclure que
, on peut en conclure que ![]() .
.
Remarque : Il y a égalité si ![]() ou
ou ![]() est nul.
est nul.
Curiosité : calculer la racine carrée d’un nombre avec une règle et un compas : explications
II – Histoire de la racine carrée
1) Les babyloniens
 Cette tablette d’argile est la plus ancienne représentation connue d’une valeur approchée de la racine carrée de deux. Elle a été écrite un scribe babylonien de la première dynastie, ce qui la situe entre 1900 et 1600 av. J.-C.
Cette tablette d’argile est la plus ancienne représentation connue d’une valeur approchée de la racine carrée de deux. Elle a été écrite un scribe babylonien de la première dynastie, ce qui la situe entre 1900 et 1600 av. J.-C.
Les trois nombres inscrits sur la tablette sont liés par la relation : ![]()
C’est-à-dire : ![]() . Ce qui se traduit par : la longueur de la diagonale d’un carré de côté 30 s’obtient en multipliant 30 par 1,41421296. Cette tablette présente donc la racine carré de 2 comme constante fondamentale de la géométrie.
. Ce qui se traduit par : la longueur de la diagonale d’un carré de côté 30 s’obtient en multipliant 30 par 1,41421296. Cette tablette présente donc la racine carré de 2 comme constante fondamentale de la géométrie.
La précision de cette valeur de la racine carrée de 2 est exceptionnelle, puisque proche du millionième. Le plus étonnant est que la valeur calculée au millième, ![]() est largement suffisante pour toutes les applications pratiques (comme par exemple l’architecture).
est largement suffisante pour toutes les applications pratiques (comme par exemple l’architecture).
2) Héron d’Alexandrie
Héron d’Alexandrie est un ingénieur, un mécanicien et un mathématicien grec du 1er siècle apr. J.-C. Il a décrit dans l’un de ses livres une méthode efficace pour calculer la racine d’un nombre mais il est probable que cette méthode était connue bien avant lui.
Chez les mathématiciens grecs, extraire la racine carrée de a revient à trouver un carré dont l’aire soit ![]() . En prenant un rectangle de côté arbitraire
. En prenant un rectangle de côté arbitraire ![]() et de même aire
et de même aire ![]() , il est nécessaire que l’autre côté ait pour longueur
, il est nécessaire que l’autre côté ait pour longueur ![]() afin que
afin que ![]() .
.
Pour le rendre « moins rectangle », il suffit de considérer un nouveau rectangle dont la longueur est la moyenne arithmétique des deux côtés précédents soit ![]() et dont l’aire fait encore
et dont l’aire fait encore ![]() .
.
En réitérant infiniment le processus, le rectangle se transforme petit à petit en un carré de même aire ![]() . Cette la méthode de Héron.
. Cette la méthode de Héron.
Utilisation de méthode de Héron pour calculer 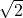 :
:
On prend, par exemple, 1 pour valeur initiale de ![]() . L’autre côté du rectangle est
. L’autre côté du rectangle est ![]() car
car ![]() .
.
La nouvelle valeur de ![]() est la moyenne des deux précédentes, soit :
est la moyenne des deux précédentes, soit : ![]() . L’autre côté du rectangle est
. L’autre côté du rectangle est ![]() car
car ![]() .
.
La valeur suivante de ![]() est la moyenne de
est la moyenne de ![]() et de
et de ![]() , soit
, soit ![]() . L’autre côté du rectangle est
. L’autre côté du rectangle est 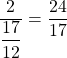 .
.
La valeur suivante de ![]() est la moyenne de
est la moyenne de ![]() et de
et de ![]() , soit
, soit ![]() à comparer avec
à comparer avec ![]() .
.
Ainsi en 3 étapes de calculs, la méthode de Héron nous fournit les 5 premières décimales de ![]() .
.
Programme Python de la méthode de Héron :
from math import *
def heron(x,a,p):
# Calcul de la racine de a par la méthode de Heron.
# Valeur initiale de l’itération : x
# Précision : 10 puissance (-p)
y = a/x
while abs(x-y) > 10**(-p):
x = (x+y)/2
y = a/x
return x

