17 page 300
On lance un dé cubique équilibré sur les faces duquel sont écrites les lettres FERMAT. On s’intéresse à la lettre obtenue sur la face supérieure.
1) Décrire l’univers, puis associer à chaque issue sa probabilité
![]()
Le dé est équilibré donc la probabilité d’obtenir chacune de ses 6 lettres différentes est la même : ![]() .
.
2) Même question si les lettres écrites sont PASCAL.
![]()
Le dé est équilibré donc la probabilité d’obtenir chacune de ses 6 faces différentes est la même. Mais deux faces possèdent la même lettre A. Par conséquent la probabilité d’obtenir la lettre A est deux fois plus importante que la probabilité d’obtenir P, S, C ou L :
![]()
20 page 300
On lance un dé à six faces numérotées de 1 à 6 et on note sa face supérieure. Le dé est truqué de telle sorte que les probabilités d’apparition de chaque face sont proportionnelles aux numéros des faces.
1) Déterminer la loi de probabilité de cette expérience.
Puisque toutes les probabilités sont proportionnelles aux numéros des faces, notons ![]() le coefficient de proportionnalité. Alors la loi de probabilité est :
le coefficient de proportionnalité. Alors la loi de probabilité est :
| Issues | 1 | 2 | 3 | 4 | 5 | 6 |
| Probabilités |
On sait par ailleurs que la somme de toutes les probabilités d’une expérience aléatoire est égale à 1. Par conséquent :
![]()
Finalement la loi de probabilité est est :
| Issues | 1 | 2 | 3 | 4 | 5 | 6 |
| Probabilités |
2) Calculer la probabilité d’obtenir un multiple de 3.
Soit A l’évènement « obtenir un multiple de 3 ». ![]() .
. ![]() .
.
36 page 302
Un sac contient des jetons numérotés. Ils sont de formes et de couleurs différentes : 40 % sont ronds, 50 % sont verts et 25 % sont ronds et verts.
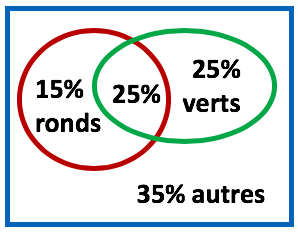 Les informations fournies permet de produire le diagramme ci-contre :
Les informations fournies permet de produire le diagramme ci-contre :
25% sont ronds et verts donc :
- 40 – 25 = 15% sont uniquement ronds
- 50 – 25 = 25% sont uniquement verts
Donc les jetons ronds, verts ou les deux représentent 15 + 25 + 25 = 65% du sac.
Ce qui permet de déduire que 100 – 65 = 35% des jetons ne sont ni ronds ni verts.
On tire un jeton au hasard. On note R l’événement « le jeton est rond » et V « le jeton est vert ». Quelle est la probabilité que ce jeton :
a) soit rond sans être vert ?
La probabilité de tirer un jeton rond sans être vert est ![]()
b) soit vert sans être rond ?
La probabilité de tirer un jeton vert sans être rond est ![]()
c) ne soit ni rond ni vert ?
La probabilité de tirer un jeton ni rond ni vert est ![]()
37 page 303
Dans un club de rugby. 20 % des adhérents sont en catégorie « poussins », 15 % en « benjamins », 45 % en « minimes » et le reste en « cadets ». Les garçons représentent 80 % des poussins, 60 % des benjamins et des minimes et 70 % des cadets. Pour représenter le club lors d’une cérémonie, on choisit au hasard un adhérent.
1) Reporter les données dans un tableau de pourcentages, puis le compléter.
Pourcentages Garçons / Filles
Ce premier tableau ne présente de difficultés. Par exemple : Si les garçons représentent 80% des poussins, 20% des poussins sont des filles.
| Poussins | Benjamins | Minimes | Cadets | |
| Garçons | 80% | 60% | 60% | 70% |
| Filles | 20% | 40% | 40% | 30% |
| Total | 100% | 100% | 100% | 100% |
Pourcentages par rapport au total d’adhérents
Quelques explications pour remplir le second tableau :
- Si les garçons représentent 80% des poussins, qui eux-mêmes représentent 20% des adhérents du club, alors
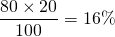 des poussins sont des garçons. On utilise ce 16% dans le calcul du 66% ci-dessous.
des poussins sont des garçons. On utilise ce 16% dans le calcul du 66% ci-dessous. - … etc …
- Pourcentage total de garçons dans le club :
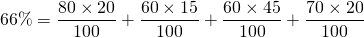 .
.
| Poussins | Benjamins | Minimes | Cadets | Total | |
| Total | 20% | 15% | 45% | 20% | 100% |
| Garçons | 16% | 9% | 27% | 14% | 66% |
| Filles | 4% | 6% | 18% | 6% | 34% |
2) Quelle est la probabilité que l’adhérent choisi :
a) soit une fille ?
La probabilité que l’adhérent choisi soit une fille est ![]() .
.
b) soit un minime ?
La probabilité que l’adhérent choisi soit un minime est ![]()
c) soit un garçon ou un minime ?
La probabilité que l’adhérent choisi soit un garçon est ![]() .
.
La probabilité que l’adhérent choisi soit un minime est ![]() .
.
La probabilité que l’adhérent choisi soit un garçon ET un minime est ![]() .
.
Donc la probabilité que l’adhérent choisi soit un garçon OU un minime est ![]() .
.
38 page 303
Pour organiser une sortie culturelle dans un groupe de 20 personnes, on pose deux questions : « Êtes-vous intéressé(e) par la musique ? » et « Êtes‑vous intéressé(e) par la lecture ? ». Huit personnes ont répondu s’intéresser à la lecture, dix à la musique. Trois personnes ont répondu positivement aux deux questions.
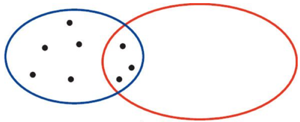 1) Reproduire, compléter et légender le diagramme suivant, qui schématise la situation.
1) Reproduire, compléter et légender le diagramme suivant, qui schématise la situation.
Ce type de représentation est appelé « diagramme de Venn », du nom d’un mathématicien et logicien anglais de la fin du XIXe siècle.
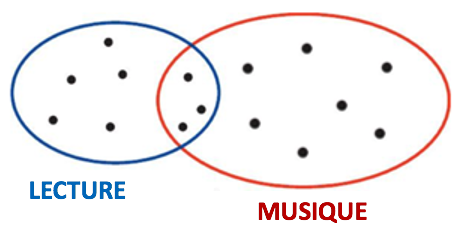 L’ovale de gauche en bleu possède 8 points dont 3 partagés avec l’ovale rouge de droite. En lisant l’énoncé, on comprend que ces 8 points représentent les 8 personnes intéressées par la lecture. 10 personnes s’intéressent à la musique dont 3 qui s’intéressent aussi à la lecture. Par conséquent les personnes intéressées que par la musique sont au nombre de 7
L’ovale de gauche en bleu possède 8 points dont 3 partagés avec l’ovale rouge de droite. En lisant l’énoncé, on comprend que ces 8 points représentent les 8 personnes intéressées par la lecture. 10 personnes s’intéressent à la musique dont 3 qui s’intéressent aussi à la lecture. Par conséquent les personnes intéressées que par la musique sont au nombre de 7
2) On choisit au hasard une personne du groupe.
a) Calculer la probabilité qu’elle s’intéresse à la musique ou à la lecture.
D’après le diagramme de Venn, on sait qu’il y a 15 personnes intéressées par la musique ou la lecture sur un total de 20. La probabilité sera donc de ![]()
b) Calculer la probabilité qu’elle ne s’intéresse ni à la musique ni à la lecture.
L’évènement « La personne ne s’intéresse ni à la musique ni à la lecture » est l’évènement contraire de l’évènement « La personne s’intéresse à la musique ou à la lecture ». La probabilité sera donc : ![]()
40 page 303
Un site Internet de vente en ligne commande une étude pour mieux comprendre les raisons des erreurs de livraison. On constate qu’il y a deux types d’erreur : erreur d’adresse postale ou erreur d’adresse mail. À partir d’études statistiques, on estime que :
- la probabilité qu’il y ait une erreur d’adresse postale est 0,08 ;
- la probabilité qu’il y ait une erreur d’adresse mail est 0,05 ;
- la probabilité qu’il y ait les deux erreurs est 0,02.
Déterminer la probabilité de chacun des événements suivants :
- E : « il y a au moins une des deux erreurs ».
- F : « il n’y a aucune erreur ».
- G : « il n’y a pas plus d’une erreur ».
- H : « il n’y a qu’une erreur ».
![]()
![]()
![]()
![]()
41 page 303
Un hôpital, situé entre deux rues parallèles, dispose de deux accueils. Marie, qui s’y rend souvent, a noté que l’accueil rue des Cerisiers était ouvert 11 fois sur 15 alors que celui de la rue des Figuiers était ouvert 7 fois sur 12. Heureusement, il y a toujours au moins un des deux accueils ouvert. Marie ne connaît pas les raisons qui conduisent l’hôpital à décider de la fermeture ou de l’ouverture d’un des accueils et elle considère que c’est aléatoire.
En prenant comme probabilité les fréquences observées, c’est-à-dire en considérant que la probabilité que l’accueil ouvert soit de ![]() pour celui de la rue des Cerisiers et de
pour celui de la rue des Cerisiers et de ![]() pour l’autre accueil, calculer la probabilité que les deux accueils soient ouverts.
pour l’autre accueil, calculer la probabilité que les deux accueils soient ouverts.
Appelons ![]() l’évènement « L’accueil des cerisiers est ouvert » et
l’évènement « L’accueil des cerisiers est ouvert » et ![]() l’évènement « L’accueil des figuiers est ouvert ».
l’évènement « L’accueil des figuiers est ouvert ». ![]() est l’évènement « les deux accueils sont ouverts ».
est l’évènement « les deux accueils sont ouverts ».
Selon l’énoncé : ![]() et
et ![]()
Par ailleurs nous savons qu’au moins un des accueils est ouvert, Donc ![]()
Or ![]() . Donc
. Donc ![]()
62 page 306
Pour organiser une sortie sur une ou deux journées, on demande aux membres d’une association de répondre à la question : « Quel(s) jour(s) êtes-vous libre ? » Voici leurs réponses :

Les organisateurs décident d’organiser la sortie dimanche.
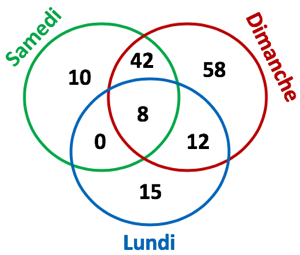 1) Combien de personnes ont répondu ?
1) Combien de personnes ont répondu ?
- On place à l’intersection des 3 cercles le nombre 8 puisque 8 personnes sont libres les 3 jours.
- On place le 15 dans la partie du cercle du lundi qui n’est pas partagée avec les deux autres cercles.
- 20 personnes sont libres au moins le dimanche et le lundi, dont 8 qui sont aussi libres le samedi donc ceux qui sont libres uniquement le lundi et le dimanche sont 12.
- Cela fait pour le lundi
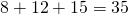 qui est le nombres des personnes libres au moins le lundi d’après le tableau. Donc il n’y a aucune personne libre le samedi et le lundi uniquement.
qui est le nombres des personnes libres au moins le lundi d’après le tableau. Donc il n’y a aucune personne libre le samedi et le lundi uniquement. - 50 personnes sont libres au moins le samedi et le dimanche dont 8 qui sont libres aussi le lundi, donc ceux qui sont libres uniquement le samedi et le dimanche sont 42.
- 120 personnes sont au moins libres le Dimanche. A partir de ce que nous avons déjà trouvé, on peut en déduire que les personnes libres uniquement le dimanche sont :
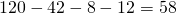 .
. - 60 personnes sont au moins libres le samedi. A partir de ce que nous avons déjà trouvé, on peut en déduire que les personnes libres uniquement le samedi sont :
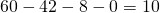 .
.
Par conséquent, le nombre de personnes ayant répondu sont au nombre de ![]() .
.
2) On choisit une personne au hasard parmi celles qui ont répondu. Quelle est la probabilité que la personne ne soit pas libre le dimanche ?
Il y a ![]() personnes libres le dimanche, donc
personnes libres le dimanche, donc ![]() qui ne le sont pas. La probabilité est :
qui ne le sont pas. La probabilité est : ![]()
Exercice n°A
Un sac opaque contient 50 jetons numérotés de 0 à 49. On prélève au hasard un jeton de ce sac et on note le numéro du jeton obtenu. On considère les évènements :
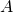 : « Le numéro obtenu est divisible par 9 »
: « Le numéro obtenu est divisible par 9 »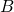 : « Le numéro obtenu est un multiple de 8 »
: « Le numéro obtenu est un multiple de 8 »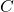 : « Le numéro obtenu est un nombre premier »
: « Le numéro obtenu est un nombre premier »
Déterminer la probabilité de chacun des évènement suivants :
Réponses :
a) ![]() Donc
Donc ![]() .Alors
.Alors ![]()
b) ![]() . Donc
. Donc ![]() . Alors
. Alors ![]()
c) ![]() . Donc
. Donc ![]()
d) ![]() . Donc
. Donc ![]()
e) Les évènements B et C n’ont aucune issue en commun car un nombre premier ne peut pas être un multiple de 8. Donc ![]()
f) Les évènements A et C n’ont aucune issue en commun car un nombre premier ne peut pas être divisible par 9. Donc ![]()
Exercice n°B
Nicolas est un astronome amateur. Il observe le ciel tous les soirs. Il constate qu’il a quatre chances sur cinq de voir Mars, une chance sur trois de voir Jupiter et trois chances sur dix de voir les deux planètes. Quelle est la probabilité que Nicolas ne voit aucune planète ce soir ?
On considère les deux évènements suivants :
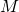 = « Voir la planète Mars ce soir ». Alors
= « Voir la planète Mars ce soir ». Alors 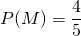
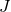 = « Voir la planète Jupiter ce soir ». Alors
= « Voir la planète Jupiter ce soir ». Alors 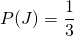
![]() est l’évènement « Voir les deux planètes ce soir ». Alors
est l’évènement « Voir les deux planètes ce soir ». Alors ![]()
On nous demande la probabilité de l’évènement A : « Ne voir aucune planète ce soir ». L’évènement contraire à A, noté ![]() , est « Voir au moins une des deux planètes ce soir ». On en déduit que
, est « Voir au moins une des deux planètes ce soir ». On en déduit que ![]() .
.
![]()
Conclusion ![]()
Exercice n°C
Dans un lycée de 1100 élèves, un sondage a été réalisé pour savoir dans quels pays, ils ont déjà séjourné. En voici les résultats :
- 20% des élèves ont séjourné en Allemagne, 28% en Espagne et 33% au Royaume-uni;
- 15% des élèves ayant séjourné en Allemagne, ont également séjourné au Royaume-uni;
- 18 élèves ont uniquement séjourné en Espagne et en Allemagne;
- Parmi ceux ayant déjà séjourné en Espagne, 26 élèves sont allés également au Royaume-uni;
- 1% des élèves ont séjourné dans ces trois pays.
On choisit un élève au hasard. On note :
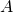 l’évènement « à déjà séjourné en Allemagne »
l’évènement « à déjà séjourné en Allemagne »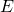 l’évènement « à déjà séjourné en Espagne »
l’évènement « à déjà séjourné en Espagne »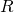 l’évènement « à déjà séjourné au Royaume-uni »
l’évènement « à déjà séjourné au Royaume-uni »
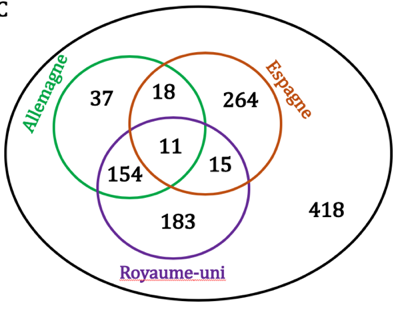 1) Représenter la situation à l’aide d’un diagramme de Venn.
1) Représenter la situation à l’aide d’un diagramme de Venn.
- 1% de élèves dans les 3 pays, soit 11 à l’intersection des 3 ovales.
- 15% des élèves en Allemagne et au R.U., soit 165. On retire les 11 également en Espagne, pour aboutir à 154.
- 18 élèves en espagne et Allemagne uniquement.
- 26 en Espagne et au R.U. On retire les 11 également en Allemagne pour aboutir à 15.
- On complète facilement avec les informations restantes : 20% des élèves ont séjourné en Allemagne, 28% en Espagne et 33% au Royaume-uni;
- On n’oublie les 418 qui n’ont été dans aucun de ces trois pays.
2) Déterminer la probabilité que l’élève :
a) ait déjà séjourné en Allemagne. ![]()
b) n’ai séjourné dans aucun de ces trois pays. ![]()
c) ai séjourné uniquement au Royaume-Uni. ![]()
d) ai séjourné uniquement dans un des trois pays. ![]()
3) Calculer les probabilités de ![]() et
et ![]() .
.
![]()
4) Calculer les probabilités ![]() et
et ![]() .
.
![]()
Exercice n°D
Jean possède un dé pipé. Il lui semble que la face 6 tombe trois fois plus que les autres faces.
1) Proposer une loi de probabilité pour modéliser cette expérience aléatoire.
Supposons que la probabilité de chacune des faces 1, 2, 3, 4 ou 5 soit ![]() . Alors d’après l’énoncé, la probabilité que la face soit 6 est
. Alors d’après l’énoncé, la probabilité que la face soit 6 est ![]() .
.
On sait que la somme des probabilités de toutes les issues d’une expérience aléatoire est 1. Donc ![]() , soit
, soit ![]() , ce qui donne
, ce qui donne ![]() . La loi de probabilité est donc :
. La loi de probabilité est donc :
| 1 | 2 | 3 | 4 | 5 | 6 |
2) Déterminer la probabilité que le résultat d’un lancer du dé soit pair.
L’évènement « lancer du dé pair » est ![]() . Sa probabilité est la somme des probabilités de ses issues, soit
. Sa probabilité est la somme des probabilités de ses issues, soit ![]() .
.
