I – Vocabulaire
- Une expérience est dite aléatoire lorsqu’elle a plusieurs issues (ou résultats) possibles et que l’on ne peut ni prévoir, ni calculer laquelle de ces issues sera réalisée.
- L’ensemble
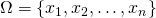 des issues possibles est appelé l’univers de cette expérience aléatoire.
des issues possibles est appelé l’univers de cette expérience aléatoire.
- Un évènement
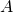 est un sous-ensemble (ou une partie) de l’univers
est un sous-ensemble (ou une partie) de l’univers 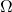 d’une expérience aléatoire. On note
d’une expérience aléatoire. On note 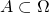 (lire :
(lire : 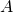 inclus dans
inclus dans 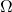 ).
). - Dire qu’une issue
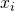 de
de 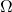 réalise l’évènement
réalise l’évènement 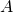 signifie que
signifie que 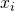 est un élément de
est un élément de 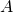 . On note
. On note 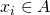 (lire :
(lire : 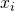 appartient à
appartient à 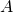 ).
).
- Le sous-ensemble
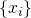 qui ne contient qu’une seule issue est appelé évènement élémentaire.
qui ne contient qu’une seule issue est appelé évènement élémentaire. - L’ensemble vide, noté
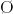 , est appelé évènement impossible : aucune issue n’appartient à cet ensemble.
, est appelé évènement impossible : aucune issue n’appartient à cet ensemble. - L’univers
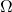 est l’évènement qui contient toutes les issues. Il est appelé évènement certain.
est l’évènement qui contient toutes les issues. Il est appelé évènement certain.
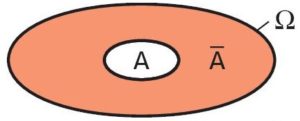 Soit
Soit 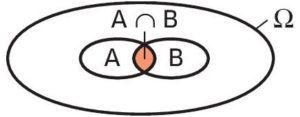 L’intersection des évènements
L’intersection des évènements 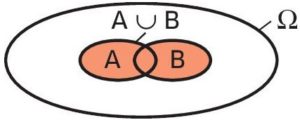 La réunion des évènements
La réunion des évènements II – Probabilités sur un ensemble fini
Expérience
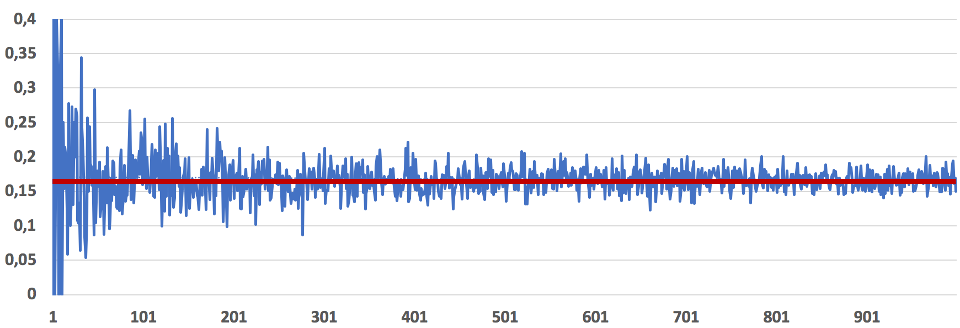
On lance ![]() fois un dé cubique dont les faces sont numérotées de 1 à 6. On observe la fréquence
fois un dé cubique dont les faces sont numérotées de 1 à 6. On observe la fréquence ![]() d’apparition de l’évènement « obtenir un 5 ». On place dans un repère orthonormé les points de coordonnées
d’apparition de l’évènement « obtenir un 5 ». On place dans un repère orthonormé les points de coordonnées ![]() pour des valeurs de
pour des valeurs de ![]() prise entre 1 et 1000. En reliant ces points on obtient la courbe bleue.
prise entre 1 et 1000. En reliant ces points on obtient la courbe bleue.
On observe expérimentalement que plus ![]() augmente, plus la fréquence
augmente, plus la fréquence ![]() se stabilise autour d’une valeur
se stabilise autour d’une valeur ![]() représenté par la droite horizontale rouge et dont la valeur est
représenté par la droite horizontale rouge et dont la valeur est ![]() , environ 0,167. Cette valeur sera appelée « probabilité de l’évènement « obtenir un 5 ».
, environ 0,167. Cette valeur sera appelée « probabilité de l’évènement « obtenir un 5 ».
Dans le suite de ce chapitre, ![]() désigne l’univers d’une expérience aléatoire.
désigne l’univers d’une expérience aléatoire.
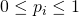 pour tous les
pour tous les 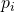
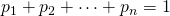
Démonstration : on sait que la somme des probabilités de toutes les issues d’une expérience aléatoire est égale à 1. Puisqu’il y a équiprobabilité, toutes les issues ont la même probabilité ![]() donc :
donc :
![Rendered by QuickLaTeX.com \[ \underbrace{p + p + \cdots + p}_{n \text{ fois}} = 1 \quad \text{soit} \quad n \imes p = 1 \quad \text{et} \quad p = \dfrac{1}{n} \]](http://www.rozenblum.com/wp-content/ql-cache/quicklatex.com-97404fef96b102697c39b4560662b356_l3.png)
Le choix du modèle peut résulter :
- d’hypothèses d’équiprobabilité : lancer d’une pièce ou d’un dé non pipé, tirer une boule au hasard dans une urne, …
- de la réalisation de l’expérience aléatoire un grand nombre de fois. On observe alors que la fréquence de chaque issue se stabilise vers un nombre que l’on choisit pour probabilité de cette issue.
III – Calculs de probabilités
Dans le suite de ce chapitre, ![]() désigne l’univers d’une expérience aléatoire.
désigne l’univers d’une expérience aléatoire.
![]()
Démonstration : Supposons que ![]() ait
ait ![]() issues. La probabilité de chaque issue est
issues. La probabilité de chaque issue est ![]() .
.
De plus, supposons que l’évènement ![]() ait
ait ![]() issues. Alors
issues. Alors
![Rendered by QuickLaTeX.com \[ P(A) = \underbrace{ \dfrac{1}{n} + \dfrac{1}{n} + \cdots + \dfrac{1}{n}}_{p \text{ fois}} = \dfrac{p}{n} \]](http://www.rozenblum.com/wp-content/ql-cache/quicklatex.com-e4bc989c5f0e40bea06edd2d1bacf65c_l3.png)
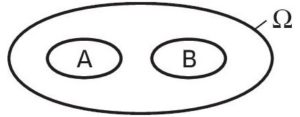 Deux évènements
Deux évènements Interprétation : ![]() et
et ![]() peuvent avoir des issues communes. Lorsqu’on écrit les issues de A et, à la suite, celles de B, on écrit deux fois les issues qui sont communes à A et B (c’est-à-dire les issues de
peuvent avoir des issues communes. Lorsqu’on écrit les issues de A et, à la suite, celles de B, on écrit deux fois les issues qui sont communes à A et B (c’est-à-dire les issues de ![]() ). C’est pour cela que l’on doit soustraire une fois la probabilité de
). C’est pour cela que l’on doit soustraire une fois la probabilité de ![]() .
.
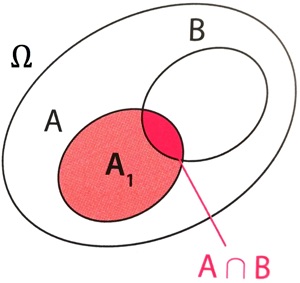
Démonstration : Soit ![]() , l’évènement formé des issues de
, l’évènement formé des issues de ![]() qui ne sont pas dans
qui ne sont pas dans ![]() .
.
Alors ![]() et
et ![]() sont incompatibles.
sont incompatibles.
Or ![]() donc
donc ![]() .
.
Ce qui donne ![]() .
.
Par ailleurs ![]() et
et ![]() sont incompatibles.
sont incompatibles.
Or ![]() donc
donc ![]()
Finalement : ![]() .
.

Démonstration : Par définition ![]() et
et ![]() sont des évènements incompatibles et
sont des évènements incompatibles et ![]() . Donc
. Donc ![]() .
.
IV – Arbre des probabilités
Un arbre des probabilité permet de décrire graphiquement une expérience aléatoire puis de calculer des probabilités d’évènements liés à cette expérience.
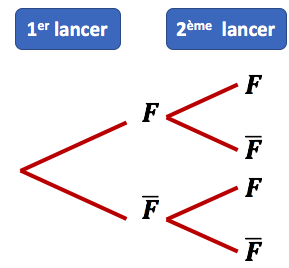 Exemple : on lance deux fois de suite une pièce équilibrée. On note
Exemple : on lance deux fois de suite une pièce équilibrée. On note ![]() l’évènement « obtenir Face » et
l’évènement « obtenir Face » et ![]() l’évènement « obtenir Pile » (qui est l’événement contraire de
l’évènement « obtenir Pile » (qui est l’événement contraire de ![]() ). L’arbre des probabilités ci-contre permet de lister les issues possibles. Il possède 4 chemins possibles.
). L’arbre des probabilités ci-contre permet de lister les issues possibles. Il possède 4 chemins possibles.
Donc l’univers est l’ensemble des couples : ![]() . Chaque issue a la même probabilité d’être réalisée. Cette probabilité vaut
. Chaque issue a la même probabilité d’être réalisée. Cette probabilité vaut ![]() .
.
L’évènement « obtenir 2 faces » correspond à un seul chemin, donc sa probabilité est ![]() .
.
L’évènement « obtenir deux faces différentes » correspond aux deux chemins ![]() et
et ![]() . Sa probabilité est alors
. Sa probabilité est alors ![]() . On remarque que la probabilité d’avoir deux faces identiques est également 0,5.
. On remarque que la probabilité d’avoir deux faces identiques est également 0,5.
V – Tableau à double entrée
Un tableau à double entrée est une autre façon de lister l’ensemble des issues d’une expérience aléatoire et de calculer des probabilités.
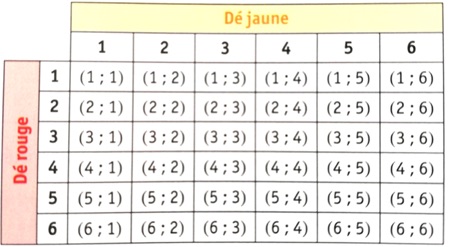
Exemple : On lance deux dés cubiques équilibrés, un rouge et un jaune. On s’intéresse au couple formé par les numéros des faces supérieures de ces dés. À l’aide du tableau à double entrée ci-contre, on recense toutes les issues possibles. On a 36 issues possibles. Chaque issue a la même probabilité d’être réalisée. Cette probabilité vaut ![]() .
.
L’évènement A « Obtenir deux nombres pairs » contient 9 issues que l’on trouve dans ce tableau. Sa probabilité est donc ![]() .
.
L’évènement B « Obtenir un 4 avec le dé rouge » contient 6 issues que l’on trouve dans ce tableau. Sa probabilité est donc ![]() .
.
L’évènement ![]() , à savoir obtenir deux nombres pairs dont le 4 avec le dé rouge. est
, à savoir obtenir deux nombres pairs dont le 4 avec le dé rouge. est ![]() . Sa probabilité est donc
. Sa probabilité est donc ![]() .
.
VI – Echantillonage
1) Introduction
Lorsqu’on étudie une grande population, il est parfois impossible de récolter toutes les données. On restreint cette étude à une partie de la population.
Exemple : si une étude porte sur la population des éléphants d’Afrique, on va limiter l’étude à une centaine d’éléphants car il est impossible de tous les étudier.
Dans le reste du chapitre, on considère une expérience aléatoire à deux issues possibles (pile ou face par exemple) que l’on répète plusieurs fois.
- On dit que l’on répète une expérience aléatoire de façon indépendante lorsque le résultat de chaque expérience ne dépend pas des résultats des expériences précédentes.
- Un échantillon de taille n est la liste des résultats obtenus lorsqu’on répète n fois une même expérience aléatoire de façon indépendante.
2) Fluctuation d’échantillonnage
On étudie le caractère d’une population donnée et on note ![]() la proportion d’individus présentant ce caractère dans la population totale. On prélève un échantillon de taille
la proportion d’individus présentant ce caractère dans la population totale. On prélève un échantillon de taille ![]() de cette population et on détermine la fréquence
de cette population et on détermine la fréquence ![]() d’apparition de ce caractère.
d’apparition de ce caractère.
On répète plusieurs fois cette opération dans les mêmes conditions et on constate que la fréquence ![]() varie suivant l’échantillon prélevé mais que cette valeur fluctue autour de la proportion
varie suivant l’échantillon prélevé mais que cette valeur fluctue autour de la proportion ![]() . Ce phénomène s’appelle la fluctuation d’échantillonnage.
. Ce phénomène s’appelle la fluctuation d’échantillonnage.
Exemple : On sait que dans une entreprise de ![]() employés , il y a 48% de femmes. La proportion de femmes est donc
employés , il y a 48% de femmes. La proportion de femmes est donc ![]() . On choisit un groupe de 100 employés et on compte le nombre de femmes. Puis on recommence l’expérience plusieurs fois. Il est clair que l’on ne va pas obtenir pour tous les groupes la même fréquence de femmes. Mais on vérifie bien que ces fréquences sont très souvent proches de 0,48.
. On choisit un groupe de 100 employés et on compte le nombre de femmes. Puis on recommence l’expérience plusieurs fois. Il est clair que l’on ne va pas obtenir pour tous les groupes la même fréquence de femmes. Mais on vérifie bien que ces fréquences sont très souvent proches de 0,48.
3) Estimation d’une probabilité par simulation
Dans certains cas, on ne connait pas la proportion d’un caractère dans une population donnée ou la probabilité de l’évènement « l’individu présence ce caractère ». Par exemple, des études ont montré que près de 40% des français sont myopes. On ne les a pas comptés un par un. On a étudié des échantillons.
Pour obtenir une estimation de la valeur ![]() , on prélève des échantillons de taille
, on prélève des échantillons de taille ![]() tel que
tel que ![]() . Si la fréquence
. Si la fréquence ![]() observée pour la présence du caractère est telle que
observée pour la présence du caractère est telle que ![]() , alors pour plus de 95% des échantillons,
, alors pour plus de 95% des échantillons, ![]() .
.
Cet intervalle est appelé intervalle de confiance de ![]() au seuil de 95%.
au seuil de 95%.
Cela signifie que :
- si la taille de l’échantillon est suffisante,
- si le caractère observé n’est ni très rare ni très fréquent
alors dans la majorité des cas, la proportion ou la probabilité du caractère sera située entre ![]() et
et ![]()
