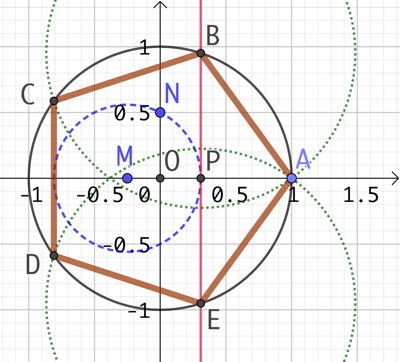
 Voici comment construire un pentagone régulier inscrit dans un cercle. Un pentagone régulier est un pentagone dont les cinq côtés ont la même longueur et les cinq angles intérieurs la même mesure :
Voici comment construire un pentagone régulier inscrit dans un cercle. Un pentagone régulier est un pentagone dont les cinq côtés ont la même longueur et les cinq angles intérieurs la même mesure :
- On trace
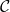 , le cercle de centre O et de longueur 1. Cette valeur arbitraire est choisie pour simplifier les calculs mais n’a aucune influence sur le procédé de construction.
, le cercle de centre O et de longueur 1. Cette valeur arbitraire est choisie pour simplifier les calculs mais n’a aucune influence sur le procédé de construction. - On place le point
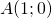 qui sera le premier des cinq sommets du pentagone. Il peut être placé n’importe où. C’est encore une fois par simplicité qu’on le place sur l’axe des abscisses.
qui sera le premier des cinq sommets du pentagone. Il peut être placé n’importe où. C’est encore une fois par simplicité qu’on le place sur l’axe des abscisses. - On place les points
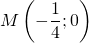 et
et 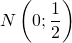 .
. - On trace le cercle de centre M passant par N. Ce cercle coupe l’axe des abscisses au point P.
- On trace la tangente du cercle au point P. Elle coupe le cercle
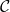 aux points B et E qui sont les deuxième et cinquième sommets du pentagone.
aux points B et E qui sont les deuxième et cinquième sommets du pentagone. - On trace un cercle de centre B passant par A. Il coupe le cercle
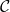 en C.
en C. - On trace un cercle de centre E passant par A. Il coupe le cercle
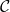 en D. On a ainsi obtenu ABCDE, un pentagone régulier inscrit dans un cercle.
en D. On a ainsi obtenu ABCDE, un pentagone régulier inscrit dans un cercle.
Explications :
La symétrie de la construction permet d’affirmer que les triangles OAB et OEA sont isométriques.
Le triangle OBC est isocèle en O. OC = OB = OA et par construction BC = BA. Donc les triangles OBC et OAB sont isométriques.
On ferait la même démonstration avec les triangles OEA et ODE.
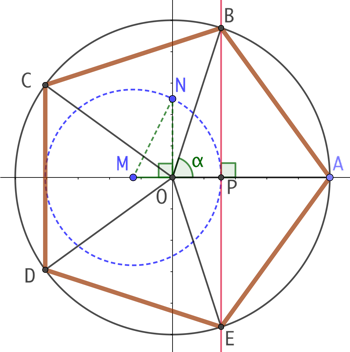
Pour démontrer que le triangle OCD est isométrique avec les quatre autres, on va démontrer que les angles au sommet de ces cinq triangles ont la même mesure.
Soit ![]() , la mesure de l’angle
, la mesure de l’angle ![]() .
. ![]() puisque OB = 1.
puisque OB = 1.
![]() puisque P et N sont sur le cercle de centre M.
puisque P et N sont sur le cercle de centre M.
MN est l’hypoténuse du triangle MON, donc 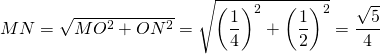 .
.
Donc ![]() (voir Triangle d’or). Sachant que
(voir Triangle d’or). Sachant que ![]() , on peut affirmer que
, on peut affirmer que ![]() .
.
Comme les triangles OAB, OBC, ODE et OEA sont isométriques, leur angle au sommet mesure ![]() . La mesure de l’angle
. La mesure de l’angle ![]() .
.
Donc le triangle OCD possède le même angle au sommet que le triangle OBC et deux côtés issus du sommet de même longueur que ceux de OBC. Ainsi les cinq triangles sont isométriques. Par conséquent les cinq côtés du pentagone ont la même longueur.
Remarque :
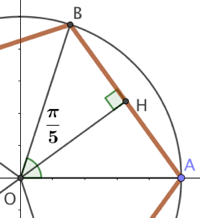
![]() .
.
![]() .
.
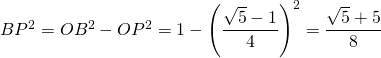 .
.
On obtient alors ![]() .
.
Autre calcul pour AB : ![]()
