 Étant donné un triangle quelconque ABC et un point D appartenant au segment [AB], où placer un point F sur le segment [BC] pour que le triangle BDF et le quadrilatère DACF aient la même aire ?
Étant donné un triangle quelconque ABC et un point D appartenant au segment [AB], où placer un point F sur le segment [BC] pour que le triangle BDF et le quadrilatère DACF aient la même aire ?
Explications :
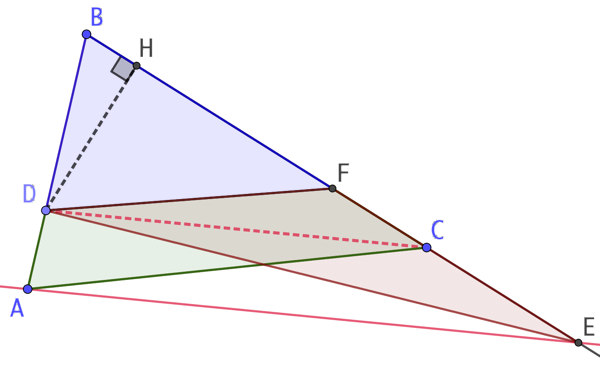
Il faut construire un triangle DEF qui possède la même aire que DACF. (Voir : Triangle d’aire égale à celle d’un quadrilatère quelconque)
On trace la parallèle à (DC) passant par A. Cette droite coupe (BC) en E.
Le triangle DEF a la même aire que DACF.
Soit H le pied de la hauteur de BDF issu de D.
L’aire de BDF est DH x BF.
L’aire de DEF est DH x FE.
Pour que ces deux aires soient égales, il faut que BF = FE, c’est à dire que F soit le milieu de [BE].
