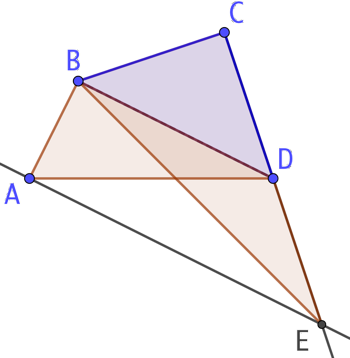
Étant donné un quadrilatère quelconque ABCD, il est possible de construire un triangle BCE de même aire que ABCD.
Construction :
- On découpe ABCD en deux triangles : BCD et ABD.
- On trace (BD) l’une des diagonales de ABCD.
- On construit la parallèle à (BD) passant par A. Celle-ci coupe la droite (CD) au point E.
Explications :
Les triangles ABD et BDE partage une même base : BD. Leurs sommets respectifs, A et E, sont situés sur une parallèle à (BD), donc ces deux triangles ont la même hauteur. Même hauteur et même base, donc même aire.
On ajoute à ces deux aires celle de BCD. Donc ABCD a la même aire que BDE.
