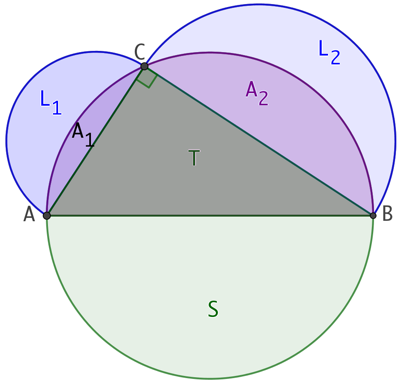
Une lunule est une figure plane en forme de croissant délimitée par deux arcs de cercle. Hippocrate a démontré que la somme des aires des deux lunules construites à partir d’un triangle rectangle est égale à l’aire de ce triangle.
Explications :
D’après le théorème de Pythagore, la somme des aires des deux demi-disques construits sur les côtés adjacents à l’angle droit d’un triangle rectangle est égale à l’aire du demi-disque construit sur son hypoténuse. Autrement dit : 
.
Par ailleurs 
. En rapprochant les deux expressions, on obtient : 
. Après simplification on obtient : 
.
Hippocrate de Chios (-470 , -410) : mathématicien grec, rédacteur d’éléments de géométrie qui ont probablement inspiré Euclide. À ne pas confondre avec Hipprocrate de Cos, le père de la médecine.
