I – Inégalité triangulaire
Nous connaissons l’affirmation « Le plus court chemin reliant deux points est la ligne droite. » Celle-ci est une conséquence d’une propriété appelée, l’inégalité triangulaire.
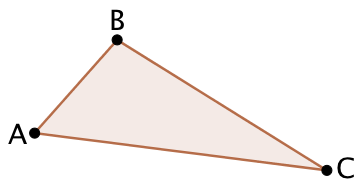 Dans un triangle, la longueur de chaque côté est inférieure à la somme des longueurs des deux autres côtés.
Dans un triangle, la longueur de chaque côté est inférieure à la somme des longueurs des deux autres côtés.
- AB < AC + CB
- AC < AB + BC
- BC < BA + BC
 Dans le cas limite où le triangle est aplati, le point B appartient au segment [AC]. Alors l’inégalité devient une égalité : AC = AB + BC.
Dans le cas limite où le triangle est aplati, le point B appartient au segment [AC]. Alors l’inégalité devient une égalité : AC = AB + BC.
On peut utiliser cette propriété pour démontrer que trois points sont alignés : Si trois points A, B et C sont tels que AC = AB + BC alors B appartient au segment [AC], c’est-à-dire que les points A, B et C sont alignés dans ce sens.
II – Construction d’un triangle
1) connaissant les longueurs de ses trois côtés
Exemple : On veut construire un triangle KLM tel que KL = 6 cm, LM = 5 cm et KM = 4,5 cm.
 |
 |
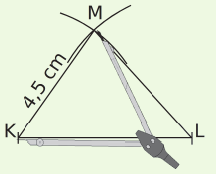 |
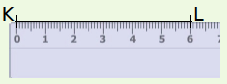
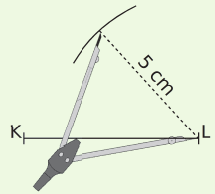
| On trace un segment [KL] de longueur 6 cm. | Le point M est à 5 cm du point L : il appartient donc au cercle de centre L et de rayon 5 cm. | Le point M est à 4,5 cm du point K : il appartient donc au cercle de centre K et de rayon 4,5 cm. Le point M est le point d’intersection des deux arcs. |
2) Connaissant la longueur d’un côté et la mesure de deux angles ayant ce côté en commun
Exemple : On veut construire un triangle KLM tel que KL = 6 cm, l’angle ![]() ° et l’angle
° et l’angle ![]() °.
°.
 |
 |
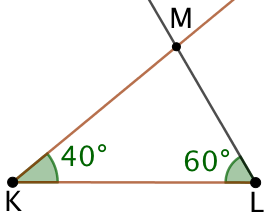 |
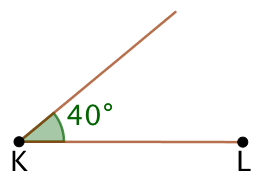
| On trace un segment [KL] de longueur 6 cm. | On trace une demi-droite de sommet K et faisant un angle de 40° avec (KL). | On trace une demi-droite de sommet L et faisant un angle de 60° avec (KL). |
L’intersection des demi-droites est le point M, troisième sommet du triangle.
3) Connaissant les longueurs de deux côtés et la mesure de l’angle délimité par ses deux côtés
Exemple : On veut construire un triangle KLM tel que KL = 6 cm, KM = 4,5 cm et l’angle ![]() °.
°.
 |
 |
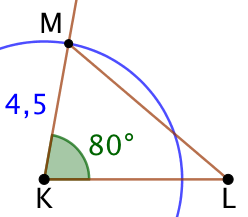 |
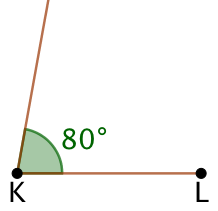
| On trace un segment [KL] de longueur 6 cm. | On trace une demi-droite de sommet K et faisant un angle de 80° avec (KL). | On trace un cercle de centre K et de rayon 4,5 cm. |
L’intersection du cercle et de la demi-droite est le point M, troisième sommet du triangle.
III – Hauteurs et aire d’un triangle
Un triangle possède trois hauteurs, chacune passant par un de ses trois sommets.
Exemples :
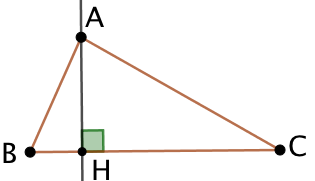 |
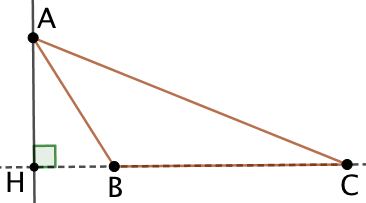 |
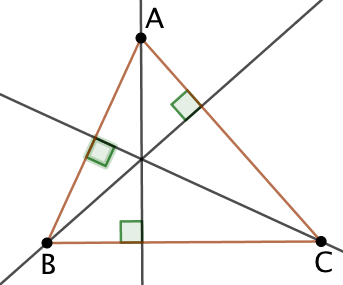 |
Si on choisit la hauteur issue de ![]() , il faut faire le calcul de l’aire avec le côté opposé à
, il faut faire le calcul de l’aire avec le côté opposé à ![]() qui est
qui est ![]() .
.
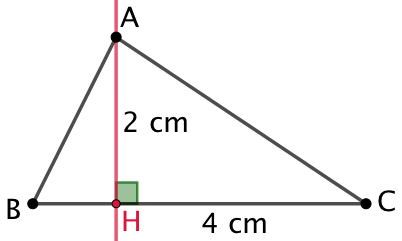 Exemple : Dans le triangle
Exemple : Dans le triangle ![]() de la figure de droite, le segment
de la figure de droite, le segment ![]() mesure 2 cm et le côté
mesure 2 cm et le côté ![]() a une longueur de 4 cm.
a une longueur de 4 cm.
Pour calculer l’aire du triangle, on effectue les deux opérations suivantes :
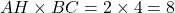
- On divise le produit obtenu par 2 :
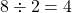
Conclusion : l’aire du triangle est 4 cm2.
Remarque : La démonstration de cette propriété sera proposée dans le chapitre sur les parallélogrammes.
EXERCICES
- 1, 3 page 117 – existence de triangles
- 8 page 117 – hauteurs
- 17 page 118 – existence triangles
- 18 page 118 – alignement
- 20 page 118 – existence quadrilatère
- 22 page 119 – existence triangles
- 66, 68 page 124 – aire
- 71 page 125 – distance
