Information chiffrée (Exercices corrigés)

24 page 270

Sur 450 personnes inscrites à un examen, 324 sont reçues. Quel est le taux de réussite ? Exprimer le résultat sous la forme d’une fraction irréductible et sous la forme d’un pourcentage.

Le taux de réussite est : $\dfrac{324}{450}$ .

Une fraction irréductible est une fraction pour laquelle le numérateur et le dénominateur n’ont aucun diviseur commun. On va donc simplifier la fraction $\dfrac{324}{450}$ pour la rendre irréductible.

$\dfrac{324}{450} = \dfrac{162 \times 2}{225 \times 2} = \dfrac{162}{225} = \dfrac{54 \times 3}{75 \times 3} = \dfrac{54}{75} = \dfrac{18 \times 3}{25 \times 3} = \dfrac{18}{25}$ .

Par ailleurs $\dfrac{18}{25} = 0,72$ . Donc le taux de réussite est aussi de 72%.

29 page 270

En 2014, 50,8 millions français avaient plus de 15 ans. 28,6 millions étaient actifs, et parmi eux, 75,2% travaillaient dans le secteur tertiaire.

1) Calculer la proportion de personnes actives dans la population des plus de 15 ans en 2014.

Le taux de personnes actives était de $\dfrac{28,6}{50,8} = 0,56$ , en valeur approchée, soit environ 56%.

2) Déterminer le nombre de personnes travaillant dans le secteur tertiaire en 2014.

On sait que 75,2% des actifs travaillaient dans le tertiaire et que la population des actifs comptait 28,6 millions de personnes. En 2014, il y avait donc dans le tertiaire $\dfrac{75,2}{100} \times 28,6 = 21,5$ millions de personnes environ.

33 page 270

Avant son déménagement, Hugo décide de se séparer de sa collection de BD. 15% de ses BD sont trop abîmées pour être vendues. Il les dépose à la déchèterie. À la braderie du village, il vend ensuite trois cinquièmes de ce qu’il lui reste. Quel pourcentage de BD rapporte-t-il chez lui à la fin de la braderie ?

Si 15% des BD sont invendables, alors 85% le sont, soit un taux de 0,85.

S’il vend trois cinquièmes des BD vendables, il lui reste deux cinquième des BD vendables. $\dfrac{2}{5} = 0,4$ .

Donc deux cinquièmes des 85% représentent un taux global de $0,4 \times 0,85 = 0,34$ .

Conclusion : il rapporte chez lui 34% des BD qu’il possédait au départ.

37 page 271

Dans un lycée, il y a 350 élèves de seconde, dont 56% de filles. Les deux cinquièmes des filles et 20% des garçons suivent une option musique. Quel est le pourcentage d’élèves de seconde qui suivent l’option musique ?

56% de filles dans le lycée, dont les deux cinquièmes font musique : $\dfrac{56}{100} \times \dfrac{2}{5} \times 350 = 0,56 \times 0,4 \times 350= 78,4$ , soit 78 filles en musique.

Les garçons représentent $100\% - 56\% = 44\%$ des 350 élèves. 20% d’entre eux font musique, soit $\dfrac{44}{100} \times \dfrac{20}{100} \times 350 = 0,44 \times 0,2 \times 350 = 30,8$ , soit 31 élèves.

Conclusion, il y a $78 + 31 = 109$ élèves sur 350 qui font musique, soit un pourcentage de $100 \times \dfrac{109}{350} = 31\%$ .

44 page 272

Dans chaque cas, calculer le taux d’évolution.

1) La population d’une ville passe de 4.000 à 9.000 habitants.

$t = \dfrac{9000 - 4000}{4000} = \dfrac{5000}{4000} = \dfrac{5}{4} = 1,25$ .

2) Un prix a été multiplié par 1,4.

On sait que le taux d’évolution et le coefficient multiplicateur sont liés par la relation : $CM = 1 +t$ . Donc $t = CM - 1 = 1,4 - 1 = 0,4$ .

3) L’association comptait 365 adhérents mais 25 en sont partis.

L’effectif a évolué de $365$ à $365 - 25$ . Donc $t = \dfrac{(365 - 25) - 365}{365} = \dfrac{-25}{365} = -0,068$ .

4) La température d’une région passe de 10°C à -10°C.

Le numérateur du taux est « température d’arrivée moins température de départ » : $t = \dfrac{-10 - 10}{10} = \dfrac{-20}{10} = -2$ .

46 page 273

Un commerçant offre à ses clients fidèles deux bons de réduction à utiliser au choix : soit 8 € de réduction sur le prix à payer, soit 12,5% sur ce même prix.

1) Quel bon de réduction a-t-on intérêt à utiliser pour un prix de 40 € ? pour un prix de 70 € ?

12,5% de 40 € représente $0,125 \times 40 = 5$ €. Le premier bon est plus intéressant. 12,5% de 70 € représente $0,125 \times 70 = 8,75$ €. Le second bon est plus intéressant.

2) Déterminer le bon à choisir suivant les valeurs du prix à payer.

Soit $p$ le prix à payer. Avec le second bon, on obtient une réduction de 12,5% de $p$ , soit $0,125 \times p$ . Le second bon est plus intéressant dès que $0,125 \times p > 8$ , soit $p > \dfrac{8}{0,125}$ , ce qui donne $p > 64$ €.

55 page 274

Un produit subit successivement une hausse de 12% puis une hausse de 8%. Calculer le taux d’évolution globale.

On rappelle la formule : $t = t_1 + t_2 + t_1t_2$ . Application numérique : $t_1 = 0,12$ et $t_2 = 0,08$ . Ce qui donne $t = 0,12 + 0,08 + 0,12 \times 0,08 = 0,2096 = 20,96\%$ .

60 page 274

Même question avec $t_1 = 25\%$ et $t_2 = -20\%$ .

Ce qui donne $t = 0,25 - 0,20 - 0,25 \times 0,20 = 0 = 0\%$ .

61 page 274

Le chiffre d’affaires (CA) d’une entreprise a diminué de 5%. Quelle augmentation du CA doit-il y avoir pour retrouver le CA initial ?

Pour revenir au CA de départ, il faut le taux global d’évolution soit 0. On pose $t_1 = -0,05$ et on cherche $t_2$ tel que $t_1 + t_2 + t_1t_2 = 0$ . Ce qui donne l’équation : $-0,05 + t_2 - 0,05t_2 = 0$ soit $0,95t_2 = 0,05$ . Ce qui donne $t_2 = \dfrac{0,05}{0,95} = 0,0526$ , soit une hausse d’environ 5,3%.

63 page 274

Sienna télécharge un nouveau jeu vidéo sur son ordinateur. Lorsque le téléchargement est terminé, l’espace libre du disque dur a diminué de 12% et il lui reste 660 Go (giga-octets) d’espace libre.

1) Quel était l’espace libre du disque dur avant le téléchargement ?

On sait d’après le cours que Si $V_0$ est l’espace de départ que l’on cherche, $V_1$ est l’espace d’arrivée (660 Go) et si $t = -12\%$ est le taux d’évolution, alors on a l’égalité : $V_1 = (1 + \dfrac{t}{100})V_0$ . Cela donne : $660 = (1 + \dfrac{-12}{100})V_0 = 0,88V_0$ . Donc $V_0 = \dfrac{660}{0,88} = 750$ Go.

2) Combien de Go occupe ce jeu vidéo ?

Puisqu’on est passé de 750 Go à 660 Go, on en conclut que le jeu occupe $750 - 660 = 90$ Go.

3) Elle télécharge un autre jeu de 99 Go. Calculer le taux de diminution de l’espace libre du disque lié à ce nouveau téléchargement.

L’espace libre passe de $660$ à $660 - 90$ . Alors le taux est $\dfrac{(660 - 99) - 660}{660} = \dfrac{-99}{660} = -0,15$ , soit $-15\%$ .

4) Calculer le taux de diminution de l’espace libre du disque lié aux deux téléchargements successifs.

À la fin du second téléchargement, il reste $660 - 99 = 561$ Go. Avant le premier téléchargement, il y avait $750$ Go. Par conséquent le taux global est $\dfrac{561 - 750}{750} = -0,252$ , soit $-25,2\%$ .

66 page 274

Début janvier 2016, il y avait 260 adhérents dans un club de tennis. Ce nombre a augmenté de 4% au cours de l’année 2016 et encore augmenté de 3% en 2017, mais a diminué de 4% en 2018.

Remarque : l’énoncé de cet exercice est très mal rédigé. Il est plus simple de répondre à la question 2 puis de revenir à la question 1

1) Calculer le taux d’évolution entre 2016 et 2019.

Le taux d’évolution entre début 2016 et début 2017 est $t_1 = 4\% = 0,04$ donc le coefficient multiplication associé est $CM_1 = 1 + t_1 = 1,04$ . Le taux d’évolution entre début 2017 et début 2018 est $t_2 = 3\% = 0,03$ donc le coefficient multiplication associé est $CM_2 = 1 + t_2 = 1,03$ . Le taux d’évolution entre début 2018 et début 2019 est $t_3 = -4\% = -0,04$ donc le coefficient multiplication associé est $CM_3 = 1 + t_3 = 0,96$ .

Par conséquent le coefficient multiplication global sur les 3 années est $CM = CM_1 \times CM_2 \times CM_3 = 1,04 \times 1,03 \times 0,96 = 1,028$ environ. Donc le taux d’évolution global sur les trois ans est $t = CM - 1 = 1,028 - 1 = 0,028 = 2,8\%$ .

2) Déterminer le coefficient multiplicateur global de l’évolution entre 2016 et 2019.

Voir réponse 1.

3) Déterminer le taux moyen d’évolution annuel.

Il suffit de diviser le taux global par le nombre d’années : $\dfrac{0,028}{3} = 0,009 = 0,9\%$ environ.

4) Déterminer le taux d’évolution réciproque de 2019 à 2016.

On commence par calculer le coefficient multiplicateur de l’évolution réciproque que l’on note CM’. Alors d’après le cours, $CM' = \dfrac{1}{CM} = \dfrac{1}{1,028} = 0,973$ environ. Donc le taux d’évolution réciproque est $t' = CM' - 1 = 0,973 - 1 = -0,027 = -2,7\%$ environ.

76 page 276

Une coopérative de fruits produit deux types de cerises : des burlats et des griottes. Les cerises qui ont un calibre trop petit seront écartées du stock et ne pourrons pas être commercialisés. On sait que 70% des cerises produits sont des burlats. Parmi les burlats, 10% sont écartées et, parmi les griottes, 25% le sont également. Quel est le pourcentage de cerises écartés du stock ?

Les burlats représentent 70% de toutes les cerises produits. 10% de ces 70% sont écartées : cela représente $0,1 \times 0,7 = 0,07 = 7\%$ de toutes les cerises produites.

Les griottes représentent 30% de toutes les cerises produits. 25% de ces 30% sont écartées : cela représente $0,25 \times 0,3 = 0,075 = 7,5\%$ de toutes les cerises produites. Conclusion $7 + 7,5 = 14,5\%$ de toutes les cerises produites sont écartées.

78 page 276

Dans une entreprise de vente par correspondance, le service courrier a remarqué que chaque lettre, qu’elle provienne de France ou de l’étranger, ne contient qu’un seul type de document, à savoir : soit une commande, soit une réclamation, soit une publicité. Une étude statistique a permis d’établir l’estimation suivante pour la répartition de l’ensemble des lettres reçues :

60% contiennent une commande et un quart des commandes vient de l’étranger;
25% contiennent une réclamation et un cinquième des réclamations vient de l’étranger;
Le reste contient de la de la publicité et provient uniquement de France.

1) Dresser un tableau qui donne la répartition pour 100 lettres reçues.

	Commandes	Réclamations	Publicités	Total
France	$60 - 15 = 45$	$25 - 5 = 20$	$15 - 0 = 15$	$100 - 20 = 80$
Étranger	$\dfrac{1}{4} \times 60 = 15$	$\dfrac{1}{5} \times 25 = 5$	0	$15 + 5 + 0 = 20$
Total	60	25	$100 - 60 - 25 = 15$	100

On peut remplir ce tableau de la façon suivante :

60% de 100 lettres contiennent une commande : 60 lettres.
Un quart des 60 commandes vient de l’étranger : 15 lettres. Donc 45 commandes viennent de France.
25% de 100 lettres contiennent une réclamation : 25 lettres.
Un cinquième des 25 réclamations vient de l’étranger : 5 lettres. 20 réclamations viennent de France.
Si sur 100 lettres, il y a 60 commandes et 25 réclamations, cela fait 15 publicités. Elles viennent toutes de France.

2) Quel pourcentage de lettres vient de France ? D’après le total de la première ligne du tableau, sur 100 lettres, 80 viennent de France. Réponse : 80%

3) Quel est le pourcentage de commandes qui provient de France ? D’après la première case du tableau, sur 100 lettres, 45 sont des commandes de France. Réponse : 45%.

4) Quel est, parmi les commandes, le pourcentage de lettre qui provient de France ? Il me semble que c’est la question 3.

80 page 277

Un examen est composé d’une épreuve pratique et d’une théorique. Pour réussir l’examen, il faut réussir chacune des deux épreuves. Cette année, la proportion de candidats ayant réussi l’épreuve pratique est égal à 0,9 ; la proportion de candidats ayant réussi l’épreuve théorique est égale à 0,8 et la proportion de candidats ayant réussi au moins une des épreuves est égale à 0,95. Calculer la proportion de candidats ayant réussi l’examen.

Pour simplifier la démonstration, on suppose qu’il y a 100 candidats en tout.

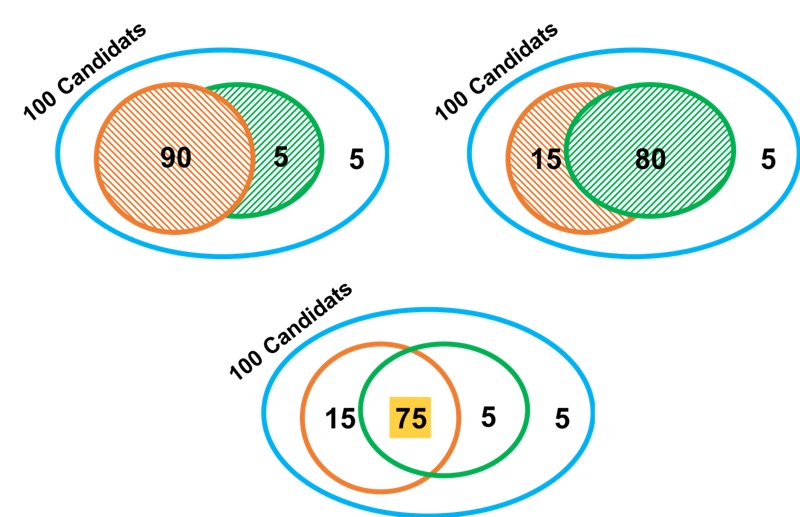
En s’aidant des 3 figures ci-dessus, on comprend que :

Première figure : 90 candidats (orange) ont réussi l’épreuve pratique et 5 candidats n’ont rien réussi, donc sur 100 candidats, il en reste 5 (vert) qui n’ont réussi que l’épreuve théorique.

Deuxième figure : 80 candidats (vert) ont réussi l’épreuve théorique et 5 candidats n’ont rien réussi, donc sur 100 candidats, il en reste 15 (orange) qui n’ont réussi que l’épreuve pratique.

Troisième figure : sur 100 candidats nous savons à présent que :

5 n’ont rien réussi ;
5 n’ont réussi que l’épreuve théorique ;
15 n’ont réussi que l’épreuve pratique.

Alors, puisque 5 + 5 + 15 = 25, on peut en conclure que 75 ont réussi les deux épreuves. Autrement dit : 75% des candidats ont réussi l’examen.

87 page 278

Un magasin propose une carte de fidélité gratuite à ses clients. Le jour de l’anniversaire de l’ouverture du magasin, les clients porteurs de la carte de fidélité bénéficient de 25% de réduction sur tous leurs achats. Par ailleurs, ce même jour, le magasin offre à tous ses clients, détenteurs ou non de la carte de fidélité, la promotion suivante sur les pantalons : « 3 pantalons achetés, le moins cher des 3 est offert ». Les deux offres ne sont pas cumulables.

1) Un client possédant la carte de fidélité arrive en caisse avec trois pantalons de même prix. Il souhaite utiliser sa carte de fidélité. Le caissier lui propose de saisir plutôt l’offre promotionnelle et de ne payer que deux pantalons. Le client préfère utiliser sa carte de fidélité. A-t-il raison ou tord ? Justifier.

Soit $p$ le prix de chaque pantalon. Le prix total est $3p$ . S’il utilise sa carte de fidélité, il aura droit à une réduction de 25% sur $3p$ , soit $0,25 \times \3p = 0,75p$ . S’il utilise la promotion, il ne paiera que le prix de 2 pantalons, ce qui correspond à une réduction égale à un pantalon, soit $p$ . Évidemment $0,75p \le p$ , donc il a tord de ne pas suivre le conseil du vendeur.

2) Un second client, qui possède aussi la carte de fidélité, se présente à la caisse avec trois pantalons de prix différents.

a) Donner un exemple de prix pour lequel il a intérêt à utiliser sa carte de fidélité. 20 €, 40 €, 60 €. Le prix total est 120 €. 25% de 120 € font $0,25 \times 120 = 30$ € de réduction par la carte. S’il utilise la promotion sur le pantalon le moins cher des trois, cela fait une réduction de 20 €.

b) Donner un exemple de prix pour lequel il a intérêt à choisir la promotion. 35 €, 40 €, 55 €. Le prix total est encore 120 €. 25% de 120 € font 30 € de réduction par la carte. S’il utilise la promotion sur le pantalon le moins cher des trois, cela fait une réduction de 35 €.

c) On désigne par $p_1, p_2, p_3$ les prix de ses trois pantalons tels que $p_1 \le p_2 \le p_3$ . À quelle condition sur ces prix, le client a-t-il intérêt à utiliser sa carte de fidélité ?

La carte de fidélité est intéressante si le pantalon le moins cher est beaucoup moins cher que les deux autres. Si les prix des pantalons sont proches, il est plus intéressant de se saisir de la promotion. Plus précisément, la promotion est plus intéressante que la carte si :

$p_3 > 0,25 \times (p_1 + p_2 + p_3)$ ,
soit $p_3 > 0,25 \times (p_1 + p_2)+ 0,25 \times p_3$ .
Ce qui donne : $p_3 - 0,25 \times p_3 > 0,25 \times (p_1 + p_2)$ ,
soit $0,75 \times p_3 > 0,25 \times (p_1 + p_2)$ ,
c’est-à-dire $p_3 > \dfrac{0,25 \times (p_1 + p_2)}{0,75}$ ,
qui se simplifie en $p_3 > \dfrac{p_1 + p_2}{3}$ .

Autrement dit, la promotion est plus intéressante que la carte de fidélité dès que le prix du pantalon le moins cher est supérieur au tiers de la somme des prix des deux autres pantalons.

Aller à la page
du cours