I – Proportionnalités (rappels)
 Exemple : On passe de la ligne des temps à la ligne des distances en multipliant la première par 80.
Exemple : On passe de la ligne des temps à la ligne des distances en multipliant la première par 80.
![]() et
et ![]() . Dans ce cas la distance parcourue est proportionnelle à la durée du déplacement. Une autre façon d’exprimer la même chose : la vitesse moyenne de la voiture est de 80 km/h.
. Dans ce cas la distance parcourue est proportionnelle à la durée du déplacement. Une autre façon d’exprimer la même chose : la vitesse moyenne de la voiture est de 80 km/h.
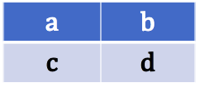 Soient quatre nombres réels quelconques
Soient quatre nombres réels quelconques Le tableau ci-contre est un tableau de proportionnalité si et seulement si ![]() .
.
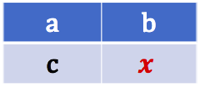 Si on connait trois des quatre nombres d’un tableau de proportionnalité,
Si on connait trois des quatre nombres d’un tableau de proportionnalité,
on peut toujours calculer le quatrième nombre : ![]()
II – Proportions et pourcentages
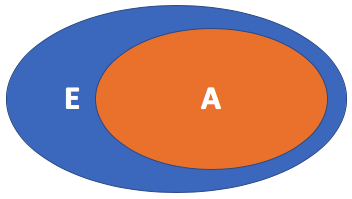 On considère un ensemble
On considère un ensemble La proportion de ![]() par rapport à
par rapport à ![]() est
est ![]() .
.
Cette proportion exprimée en pourcentage est ![]() .
.
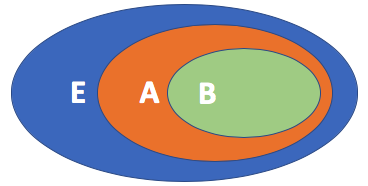 On considère un ensemble
On considère un ensemble Si la proportion de ![]() par rapport à
par rapport à ![]() est
est ![]() et la proportion de
et la proportion de ![]() par rapport à
par rapport à ![]() est
est ![]() ,
,
alors la proportion des éléments de ![]() dans
dans ![]() est
est ![]() .
.
Démonstration :
Soient ![]() et
et ![]() les nombres d’éléments respectifs de
les nombres d’éléments respectifs de ![]() et
et ![]() .
.
Par définition, la proportion de ![]() par rapport à
par rapport à ![]() est
est ![]() et la proportion de
et la proportion de ![]() par rapport à
par rapport à ![]() est
est ![]() .
.
Donc la proportion de ![]() par rapport à
par rapport à ![]() est
est ![]() .
.
On sait que ![]() ,
, ![]() et
et ![]() . Donc
. Donc ![]() ,
, ![]() et
et ![]()
En injectant ces résultats dans la formule ![]() , il vient
, il vient ![]() .
.
Exemple : Dans un lycée de 800 élèves, 25 % des élèves sont en Seconde et 45 % des élèves de Seconde sont des filles. La part des filles de Seconde dans le lycée est de ![]() .
.
III – Pourcentages d’évolution
On considère une quantité passant d’une valeur ![]() à une valeur
à une valeur ![]() .
.
On a donc : ![]() .
.
Exemple n°1 : Si, sur une période de temps donnée, le nombre d’habitants d’une ville passe de 12000 à 15000, alors le coefficient multiplicateur sera : ![]() . Autrement dit, partant de 12000, on arrive à 15000 en multipliant 12000 par 1,25.
. Autrement dit, partant de 12000, on arrive à 15000 en multipliant 12000 par 1,25.
Exemple n°2 : Si, sur une période de temps donnée, le nombre d’habitants d’une ville passe de 15000 à 12000, alors le coefficient multiplicateur sera : ![]() . Autrement dit, partant de 15000, on arrive à 12000 en multipliant 15000 par 0,8.
. Autrement dit, partant de 15000, on arrive à 12000 en multipliant 15000 par 0,8.
Démonstration : S’il y a une augmentation, alors ![]() donc
donc ![]() . C’est-à-dire que
. C’est-à-dire que ![]() .
.
Démonstration similaire dans le cas d’une diminution.
- La variation absolue entre
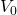 et
et 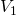 est :
est : 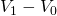 .
. - La variation relative ou le taux d’évolution entre
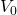 et
et 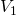 est :
est : 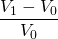 .
. - Le taux d’évolution exprimé en pourcentage est :
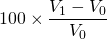 .
.
Démonstration : S’il y a augmentation alors nous savons que ![]() , c’est-à-dire que
, c’est-à-dire que ![]() donc
donc ![]() , soit
, soit ![]() . Ce qui aboutit à
. Ce qui aboutit à ![]() .
.
Démonstration similaire dans le cas d’une diminution.
Exemple : Le prix d’un article passe de 80€ à 76€. Le taux d’évolution est : ![]() .
.
Le coefficient multiplicateur est : ![]() .
.
Si ![]() est exprimé en pourcentage, l’égalité s’écrit :
est exprimé en pourcentage, l’égalité s’écrit : ![]() .
.
Démonstration : ![]() .
.
Si ![]() est exprimé en pourcentage, l’égalité s’écrit :
est exprimé en pourcentage, l’égalité s’écrit : ![]() .
.
Démonstration : ![]() . Donc
. Donc ![]() .
.
- Pour obtenir
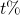 de
de 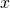 , on multiplie
, on multiplie 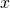 par
par 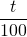 .
. - Pour augmenter
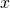 de
de 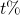 , on multiplie
, on multiplie 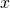 par
par 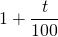 .
. - Pour diminuer
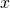 de
de 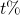 , on multiplie
, on multiplie 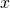 par
par 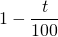 .
.
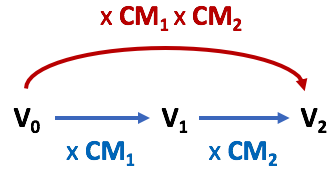
Démonstration pour deux évolutions :
Première évolution : ![]()
Deuxième évolution : ![]() .
.
Remarque importante : Si ![]() et
et ![]() sont les taux d’évolution alors
sont les taux d’évolution alors ![]() et
et ![]() .
.
Le coefficient multiplicateur global est donc ![]() .
.
Soit t le taux d’évolution global. Alors ![]() .
.
Si les taux d’évolution sont exprimés en pourcentages, cela donne : ![]() , soit après multiplication par 100 :
, soit après multiplication par 100 : ![]() .
.
ATTENTION : Cela illustre l’erreur souvent faite qui consiste à croire que le pourcentage global est la somme des deux pourcentages de deux évolutions successives. En faisant ainsi on oublie le terme ![]() .
.
Exemple : Le prix d’un objet augmente de 10% puis diminue de 10%.
Donc ![]() et
et ![]()
Soit ![]() le taux d’évolution global.
le taux d’évolution global. ![]() . Le prix de l’objet a globalement diminué de 1%.
. Le prix de l’objet a globalement diminué de 1%.
Une hausse de t % ne « compense » pas une baisse de t %. C’est dû au fait que les deux pourcentages ne portent pas sur le même montant. En cas d’évolution successives, les pourcentages d’évolutions ne s’ajoutent (ni ne soustraient) jamais.
IV – Évolution réciproque
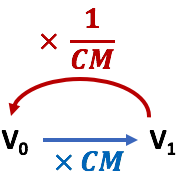 Démonstration : Par hypothèse
Démonstration : Par hypothèse ![]() et
et ![]() .
.
Donc ![]() . En simplifiant par
. En simplifiant par ![]() , il reste
, il reste ![]() , soit
, soit ![]() .
.
- Soit
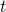 et
et 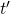 les taux d’évolution correspondant à une évolution et à sa réciproque. De l’égalité
les taux d’évolution correspondant à une évolution et à sa réciproque. De l’égalité 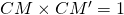 , il vient
, il vient 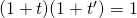 .
. - Avec des taux exprimés en pourcentage, l’égalité devient :
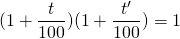 .
.
Démonstration : conséquences de la propriété précédente.
Exemple : Le prix d’un article augmente de 60%. Quelle baisse faut-il appliquer pour qu’il revienne à son prix de départ ?
On pose ![]() et
et ![]() le taux de baisse recherché.
le taux de baisse recherché.
On a donc ![]() . Ce qui donne
. Ce qui donne ![]() , soit
, soit ![]() . Donc
. Donc ![]() . On obtient
. On obtient ![]() .
.
Il faut donc que le prix diminue de 37,5% pour compenser la hausse de 60%.

