
I. PYRAMIDE
1) Définition :
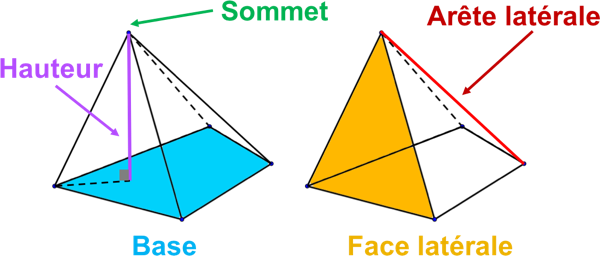 Une pyramide est un solide dans lequel :
Une pyramide est un solide dans lequel :
- une des faces, appelée base de la pyramide, est un polygone ;
- les autres faces, appelées faces latérales, sont des triangles qui ont un sommet commun, appelé sommet de la pyramide.
La hauteur d’une pyramide est le segment issu de son sommet et perpendiculaire à sa base.
Une arête latérale est un segment joignant un des sommets de la base au sommet de la pyramide.
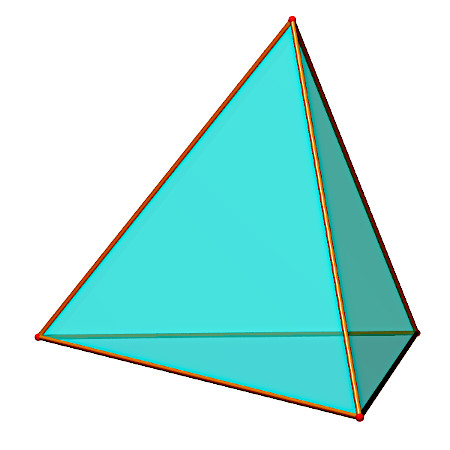
Exemple : Un tétraèdre est une pyramide dont la base est un triangle
2) Pyramide régulière :
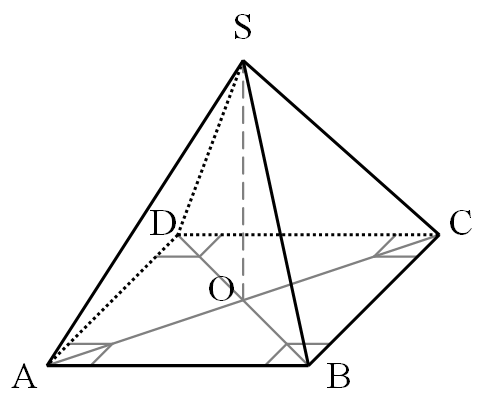 Une pyramide régulière est une pyramide dont la base est un polygone régulier et dont les faces latérales sont des triangles isocèles et superposables.
Une pyramide régulière est une pyramide dont la base est un polygone régulier et dont les faces latérales sont des triangles isocèles et superposables.
La hauteur d’une pyramide régulière passe par le centre de la base. On démontre que le centre de la base est le centre du cercle circonscrit à cette base, c’est-à-dire le cercle passant par les sommets de la base.
Exemple : une pyramide dont la base est un carré.
3) Patron d’une pyramide :
Voici le patron d’une pyramide régulière à base carrée :
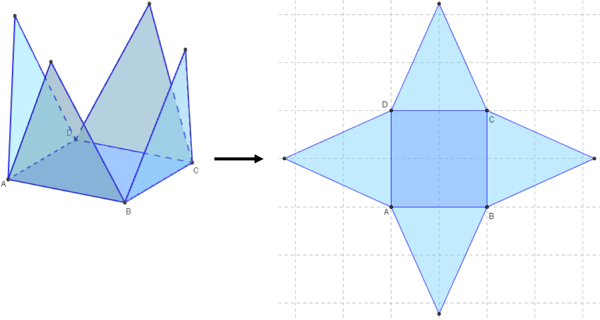
Et voici le patron d’une pyramide régulière dont la base est triangle équilatéral :
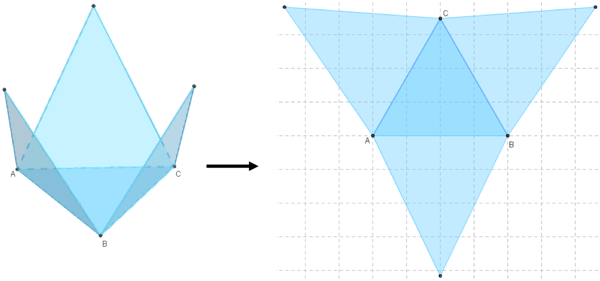
La vidéo suivante explique comment tracer le patron d’un prisme (programme de cinquième) et celui d’une pyramide.
4) Volume d’une pyramide :
Alors le volume de la pyramide est :
Si la hauteur est exprimée en m et la base en m2, alors le volume est exprimé en m3.
Exemple : Quel est le volume d’une pyramide de hauteur 2,5 m et de base un rectangle de dimensions 4 m et 4,20 m ?
L’aire de la base est ![]() .
.
Le volume est ![]() m3.
m3.
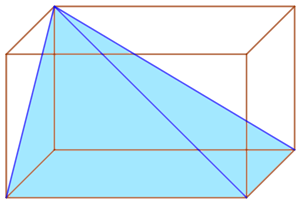 Remarque : Si une pyramide est inscrite dans un prisme, c’est-à-dire si on place une pyramide dans un prisme dont la base est identique à celle de la pyramide et la hauteur égale à celle de la pyramide, alors le volume du prisme est le triple de celui de la pyramide.
Remarque : Si une pyramide est inscrite dans un prisme, c’est-à-dire si on place une pyramide dans un prisme dont la base est identique à celle de la pyramide et la hauteur égale à celle de la pyramide, alors le volume du prisme est le triple de celui de la pyramide.
Le volume de la pyramide bleue est ![]() . Le parallélépipède a la même base
. Le parallélépipède a la même base ![]() et la même hauteur
et la même hauteur ![]() . Donc son volume est
. Donc son volume est ![]() qui est bien le triple de celui de la pyramide.
qui est bien le triple de celui de la pyramide.
La vidéo suivante montre la relation entre le volume d’une pyramide carrée et de hauteur égale au côté de sa base d’une part, et le volume d’un cube dont le côté est égale au côté de la base de la pyramide, d’autre part.
II. CÔNE DE RÉVOLUTION
1) Définition :
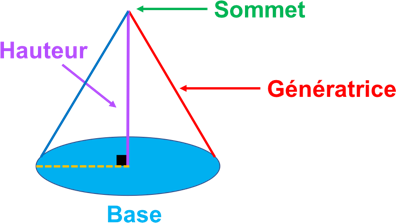 Un cône de révolution est un solide obtenu en faisant tourner un triangle rectangle autour d’un des côtés de son angle droit.
Un cône de révolution est un solide obtenu en faisant tourner un triangle rectangle autour d’un des côtés de son angle droit.
La base d’un cône de révolution est un disque. (Dans le dessin de droite, la base est représentée sous la forme d’une ellipse car c’est une vue en perspective.)
La hauteur d’un cône de révolution est le segment qui joint le centre de ce disque au sommet du cône. Ce segment est perpendiculaire à la base.
Une génératrice d’un cône de révolution est un segment qui joint le sommet du cône à un point du cercle de sa base.
Ci-dessous une animation montrant un triangle rectangle pivotant autour de l’un des côtés de son angle droit :
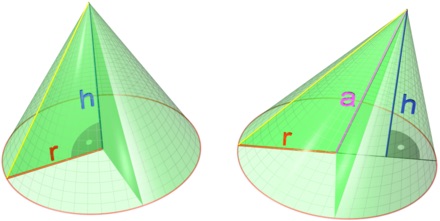
Dans la figure ci-contre, le cône de gauche est un cône de révolution. Par contre le cône de droite n’est pas un cône de révolution car sa hauteur ne passe pas par le centre du cercle de sa base.
2) Longueur d’un secteur :
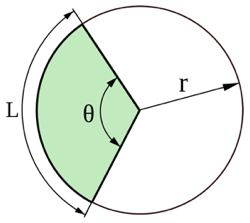 Un secteur circulaire est la partie d’un disque délimitée par deux rayons et un arc de cercle.
Un secteur circulaire est la partie d’un disque délimitée par deux rayons et un arc de cercle.
Dans la figure ci-contre, on a représenté en vert un secteur défini par son angle d’ouverture ![]() . La longueur L du secteur est proportionnelle à l’angle
. La longueur L du secteur est proportionnelle à l’angle ![]() .
.
| Angle (degré) | 360 | |
| L |
De cette formule on en déduit une autre utile pour réaliser le patron d’un cône de révolution :
![]() .
.
3) Patron d’un cône de révolution :
 Le patron d’un cône de révolution se compose de deux parties :
Le patron d’un cône de révolution se compose de deux parties :
- un disque qui est la base du cône
- un secteur (une partie de disque) correspondant à la surface formée par la génératrice.
Supposons que le rayon du cercle de base soit ![]() et la longueur de la génératrice soit
et la longueur de la génératrice soit ![]() . On sait que le périmètre du cercle de base est
. On sait que le périmètre du cercle de base est ![]() . La longueur du secteur est égale au périmètre du cercle de base. Donc d’après ce qui a été vu au paragraphe précédent, l’angle du secteur est
. La longueur du secteur est égale au périmètre du cercle de base. Donc d’après ce qui a été vu au paragraphe précédent, l’angle du secteur est ![]() .
.
Comme ![]() , on obtient
, on obtient ![]() .
.
La procédure de construction est la suivante :
- On trace le cercle de la base du cône de rayon
 .
. - On trace un rayon de ce cercle.
- On prolonge ce rayon d’une longueur
 égale à celle de la génératrice.
égale à celle de la génératrice.  est le rayon du secteur.
est le rayon du secteur. - On trace un secteur de rayon
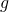 et d’angle
et d’angle 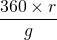 .
.
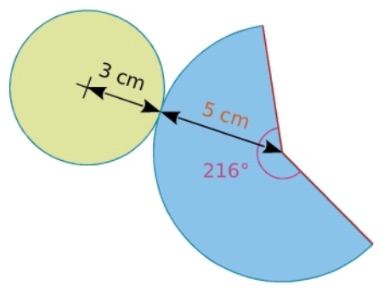 Exemple : On veut produire le patron d’un cône de rayon 3 cm et de génératrice 5 cm.
Exemple : On veut produire le patron d’un cône de rayon 3 cm et de génératrice 5 cm.
- On trace un cercle de rayon 3 cm qui est la base du cône.
- On prolonge un rayon du cercle d’une longueur de 5 cm.
- L’angle du secteur est
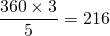 .
. - On trace un cercle de rayon 5 cm.
- On ne conserve que
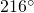 de ce cercle.
de ce cercle.
4) Volume d’un cône de révolution :
Si le rayon et la hauteur sont exprimés en m, alors le volume est exprimé en m3.
Exemple : Quel est le volume d’un cône de rayon 5 cm et de hauteur 10 cm ?
Le volume est ![]() cm3 environ.
cm3 environ.
III. SECTIONS
1) Définition :
 La section d’un solide par un plan est l’intersection entre ce solide et ce plan
La section d’un solide par un plan est l’intersection entre ce solide et ce plan
2) Propriétés :
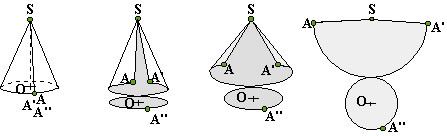
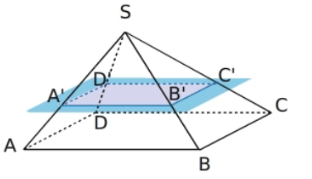
La section d’une pyramide par un plan parallèle à sa base est un polygone de même nature que la base.
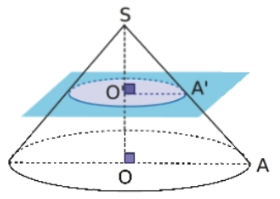
La section d’un cône de révolution par un plan parallèle à sa base est un disque de rayon inférieur à celui de sa base.
 |
 |

