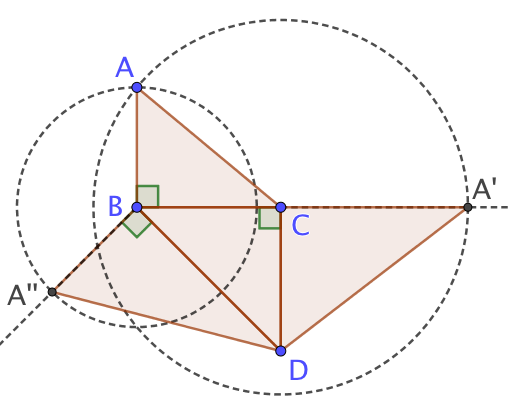
Exercice n°2 page 140
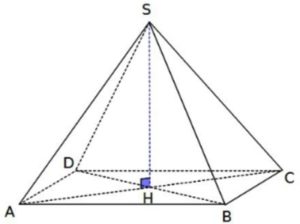 Une pyramide régulière a pour base un carré de côté 5 cm et pour hauteur 6 cm.
Une pyramide régulière a pour base un carré de côté 5 cm et pour hauteur 6 cm.
a) Donne les longueurs BC et CH :
Voir le corrigé
BC est un côté de la base donc BC = 5 cm et SH est la hauteur, donc SH = 6 cm.
b) Combien ce solide possède-t-il d’arêtes ? De faces ? De sommets :
Voir le corrigé
8 arêtes dont 4 latérales, 5 faces dont 4 latérales, 5 sommets dont 4 qui appartiennent à la base.
c) Indique toutes les égalités de longueurs : Voir le corrigé
La base est carrée donc AB = BC = CD = DA et AC = DB. À partir du sommet on a : SA = SB = SC = SD.
d) Donne l’aire de la face ABCD :
Voir le corrigé
c’est l’aire d’un carré de côté 5 cm, ce qui donne 25 cm2
.
e) Donne le volume de cette pyramide :
Voir le corrigé
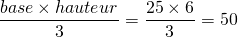
cm
3.
Exercice n°4 page 140
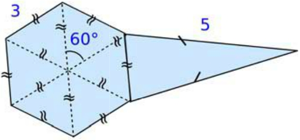 a) De quel solide a-t-on commencé le patron ?
a) De quel solide a-t-on commencé le patron ?
Voir le corrigé
Une pyramide régulière dont la base est un hexagone régulier.
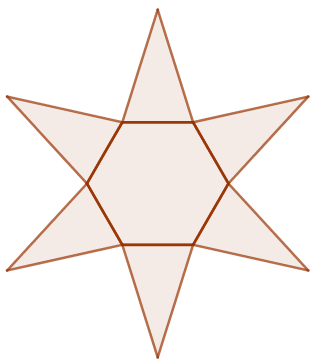 b) Combien ce solide possède-t-il d’arêtes ? de faces ? de sommets ?
b) Combien ce solide possède-t-il d’arêtes ? de faces ? de sommets ?
Voir le corrigé
Il possède :
- 12 : 6 arêtes latérales et 6 arêtes qui sont les côtés de la base hexagonale.
- 7 : 6 faces latérales plus la base.
- 7 : 1 sommet de la pyramide et les 6 sommets de la base hexagonale.
c) Que faut-il construire pour terminer ce patron ?
Voir le corrigé
5 faces latérales en forme de triangle isocèle de côtés mesurant 5, 5 et 3 unités.
Ci-contre un exemple du patron complet.
Exercice n°10 page 141
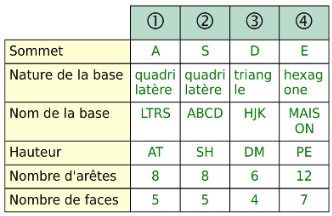
Recopie et complète le tableau ci-dessous.
Exercice n°16 page 142
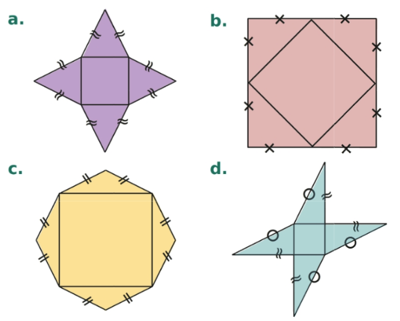 Parmi les 4 figures, quels sont les patrons d’une pyramide à base carrée.
Parmi les 4 figures, quels sont les patrons d’une pyramide à base carrée.
Voir le corrigé
Seule la figure a. est un patron de pyramide carrée.
Les faces latérales triangulaires des figures b. et c. ne sont pas assez grandes pour que la pyramide se referme. Les faces triangulaires de la figure d. ne sont pas isocèles.
Exercice n°18 page 142
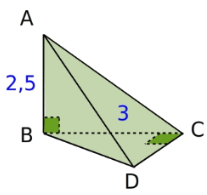 ABCD est une pyramide dont la base est un triangle rectangle isocèle en C tel que AB = 2,5 cm et BC = 3 cm. Construis un patron de cette pyramide.
ABCD est une pyramide dont la base est un triangle rectangle isocèle en C tel que AB = 2,5 cm et BC = 3 cm. Construis un patron de cette pyramide.
Exercice n°21 page 143
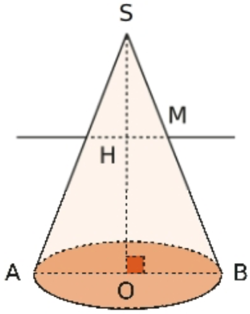 On considère le cône de révolution ci-contre tel que
On considère le cône de révolution ci-contre tel que 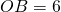 cm et
cm et 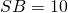 cm.
cm.
a) Calculer la hauteur 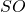 du cône.
du cône.
Voir le corrigé
Le théorème de pythagorean appliqué au triangle rectangle SOB donne l’égalité :
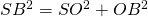
.
Donc 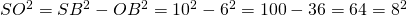 .
.
Par conséquent 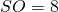 cm.
cm.
b) Calculer l’angle 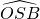
Voir le corrigé
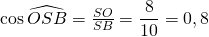
.
Par conséquent 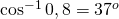 environ.
environ.
c) Soit M un point de la génératrice (SB) tel que 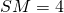 cm. On trace une droite parallèle à (OB) passant par M. Elle coupe (SO) en H. Montrer que (SO) et (HM) sont perpendiculaires.
cm. On trace une droite parallèle à (OB) passant par M. Elle coupe (SO) en H. Montrer que (SO) et (HM) sont perpendiculaires.
Voir le corrigé
(HM) est parallèle (OB). or (OB) est perpendiculaire à (OS). Donc (HM) est perpendiculaire à (OS).
d) Calculer HM et SH.
Exercice n°26 page 144
Pour construire la pyramide de Khéops, les Égyptiens ont utilisé environ 2 643 000 m3 de pierres. La hauteur de la pyramide est de 146 m. Calcule le côté du carré constituant la base de la pyramide. Arrondis ton résultat au mètre.
 Exercice n°30 page 144
Exercice n°30 page 144
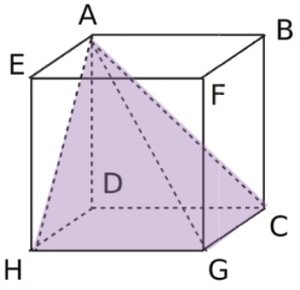
ACDHG est une pyramide inscrite dans un cube de côté 4 cm.
a) Calcule le volume de cette pyramide arrondi au cm3.
Voir le corrigé
Le volume de la pyramide est le tiers de celui du cube dans lequel elle est inscrite, soit 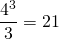 cm3.
cm3.
b) Calcule les longueurs AH, DG et AG, arrondies au mm.
Voir le corrigé
[AH] est l’hypoténuse du triangle ADH rectangle en D. Donc on applique le théorème de Pythagore :
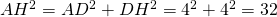
. Ce qui donne
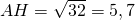
cm.
[DG] est l’hypoténuse du triangle DHG rectangle en H. Tous ces calculs se fond dans un cube dont les faces sont des carrés identiques. Donc
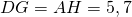
cm.
[AG] est l’hypoténuse du triangle ADG rectangle en D. Donc
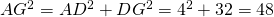
. Ce qui donne
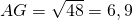
cm.
c) Détermine la mesure de l’angle 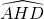 .
.
Voir le corrigé
Toutes les faces du cube sont des carrés. Donc EHDA est un carré. La diagonale [AH] de ce carré est aussi la bissectrice de l’angle 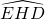 qui est un angle droit. Alors
qui est un angle droit. Alors 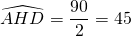 .
.
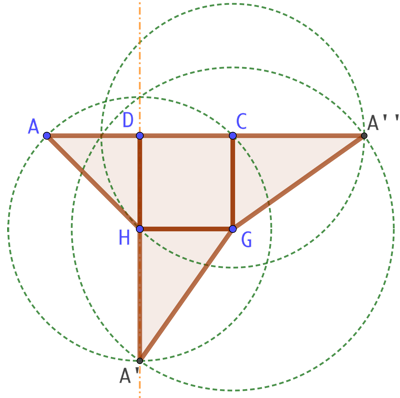 d) Construis un patron de cette pyramide.
d) Construis un patron de cette pyramide.
Exercice supplémentaire n°1
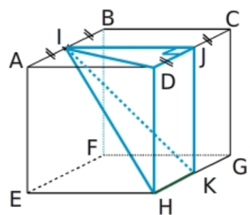 ABCDEFGH est un cube de côté 8 cm.
ABCDEFGH est un cube de côté 8 cm.
Calculer le volume exact de IJDHK.
Exercice supplémentaire n°2
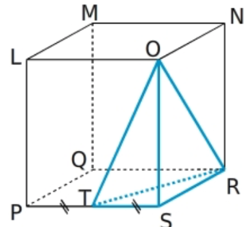 LMNOPQRS est un pavé droit tel que LM = 5 cm, LO = 5,6 cm et LP = 8,6 cm.
LMNOPQRS est un pavé droit tel que LM = 5 cm, LO = 5,6 cm et LP = 8,6 cm.
Calculer le volume exact de ORST.
Exercice supplémentaire n°3
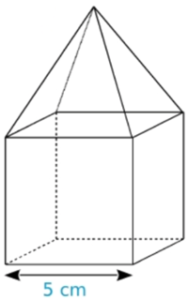 Voici un solide composé d’un cube et d’une pyramide dont la hauteur est la même que celle du cube. Calculer son volume exact.
Voici un solide composé d’un cube et d’une pyramide dont la hauteur est la même que celle du cube. Calculer son volume exact.
Voir le corrigé
Le cube et la pyramide ont la même hauteur et la même base. Donc la pyramide est inscrite dans le cube. Par conséquent la pyramide a un volume égal au tiers de celui du cube.
Le volume du cube est : 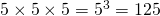 cm3. Donc le volume de la pyramide est de
cm3. Donc le volume de la pyramide est de 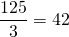 cm3 environ.
cm3 environ.
Ainsi le solide dans son ensemble aura un volume de 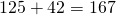 cm3 environ.
cm3 environ.
Exercice supplémentaire n°4
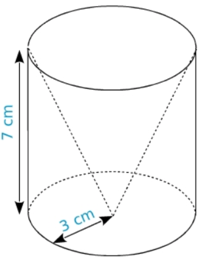 Voici un cylindre contenant un cône de révolution. Quel est le volume du solide dont on a retiré le cône ?
Voici un cylindre contenant un cône de révolution. Quel est le volume du solide dont on a retiré le cône ?
Voir le corrigé
Le volume du cône est : 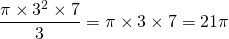 cm3.
cm3.
Le volume du cylindre est : 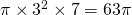 cm3. On vérifie ainsi que le cylindre contenant le cône a un volume trois fois supérieur à celui du cône.
cm3. On vérifie ainsi que le cylindre contenant le cône a un volume trois fois supérieur à celui du cône.
Si on retire le volume du cône du volume du cylindre, on obtient 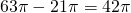 cm3.
cm3.
 Aller à la page
Aller à la page
du cours
 Une pyramide régulière a pour base un carré de côté 5 cm et pour hauteur 6 cm.
Une pyramide régulière a pour base un carré de côté 5 cm et pour hauteur 6 cm. a) De quel solide a-t-on commencé le patron ?
a) De quel solide a-t-on commencé le patron ? b) Combien ce solide possède-t-il d’arêtes ? de faces ? de sommets ?
b) Combien ce solide possède-t-il d’arêtes ? de faces ? de sommets ?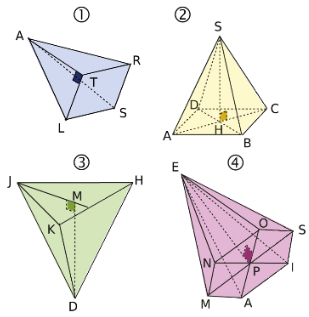
 Parmi les 4 figures, quels sont les patrons d’une pyramide à base carrée.
Parmi les 4 figures, quels sont les patrons d’une pyramide à base carrée. ABCD est une pyramide dont la base est un triangle rectangle isocèle en C tel que AB = 2,5 cm et BC = 3 cm. Construis un patron de cette pyramide.
ABCD est une pyramide dont la base est un triangle rectangle isocèle en C tel que AB = 2,5 cm et BC = 3 cm. Construis un patron de cette pyramide. On considère le cône de révolution ci-contre tel que
On considère le cône de révolution ci-contre tel que ![]() cm et
cm et ![]() cm.
cm.![]() du cône.
du cône.![]()
![]() cm. On trace une droite parallèle à (OB) passant par M. Elle coupe (SO) en H. Montrer que (SO) et (HM) sont perpendiculaires.
cm. On trace une droite parallèle à (OB) passant par M. Elle coupe (SO) en H. Montrer que (SO) et (HM) sont perpendiculaires. Exercice n°30 page 144
Exercice n°30 page 144![]() .
. d) Construis un patron de cette pyramide.
d) Construis un patron de cette pyramide. ABCDEFGH est un cube de côté 8 cm.
ABCDEFGH est un cube de côté 8 cm. LMNOPQRS est un pavé droit tel que LM = 5 cm, LO = 5,6 cm et LP = 8,6 cm.
LMNOPQRS est un pavé droit tel que LM = 5 cm, LO = 5,6 cm et LP = 8,6 cm. Voici un solide composé d’un cube et d’une pyramide dont la hauteur est la même que celle du cube. Calculer son volume exact.
Voici un solide composé d’un cube et d’une pyramide dont la hauteur est la même que celle du cube. Calculer son volume exact. Voici un cylindre contenant un cône de révolution. Quel est le volume du solide dont on a retiré le cône ?
Voici un cylindre contenant un cône de révolution. Quel est le volume du solide dont on a retiré le cône ?