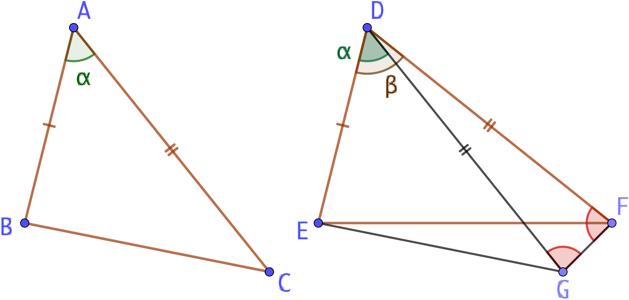
 Soient deux triangles isocèles ABC et DEF tels que AB = DE, AC = DF et
Soient deux triangles isocèles ABC et DEF tels que AB = DE, AC = DF et ![]() ; alors BC < EG.
; alors BC < EG.
Explications :
On place le point G tel que DEG soit isométrique à ABC. Puisque DF = DG, le triangle DGF est isocèle en D et par conséquent ![]() .
.
Mais ![]() et
et ![]() .
.
Donc ![]() .
.
Comme le plus grand côté fait face au plus grand angle, on en conclut que EG < EF, soit BC < EG.
Remarque : La réciproque de ce résultat s’établit facilement par un raisonnement par l’absurde.
Remarque : Il s’agit des propositions n°I.24 et I.25 des Éléments d’Euclide.
