On sait que dans un triangle isocèle en A, les angles opposés au sommet A sont de même mesure : Angles égaux d’un triangle isocèle.par
On démontre qu’un triangle possédant deux angles de même mesure est isocèle.
Explications :
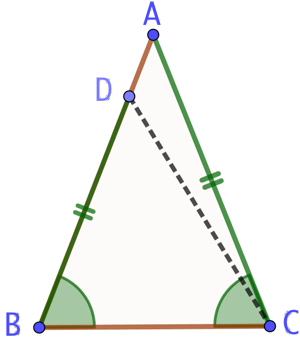
Supposons que ABC n’est pas isocèle et, que par exemple, AB > AC. Soit alors le point D du segment [AB] tel que AC = DB.
On constate alors que les triangles DBC et ABC sont isométriques car :
- Ils ont deux côtés égaux de même longueur : AC = BD et un côté en commun BC ;
- par hypothèse, l’angle délimité par ces côtés égaux sont de même mesure :
;
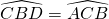Or le petit triangle DBC ne peut être isométrique au grand triangle ABC.
Conclusion : les côtés AB et AC ont la même longueur.
Remarque : Il s’agit de la proposition I.6 des Éléments d’Euclide.
