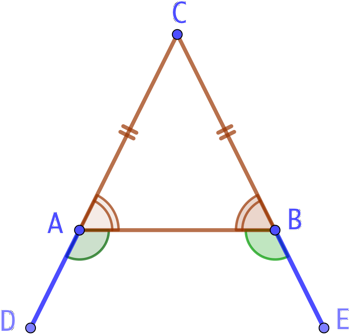
Les deux angles à la base d’un triangle isocèle sont de même mesure.
Explications :
 |
 |
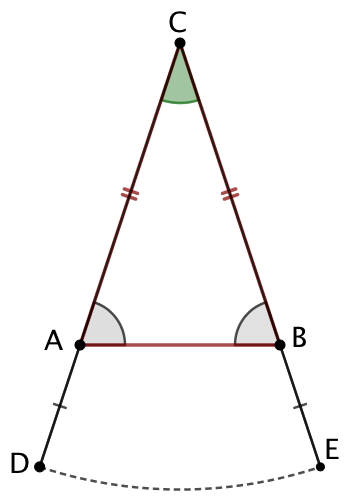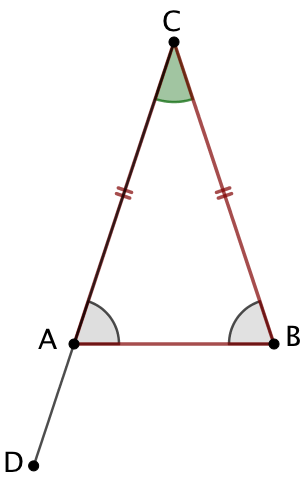
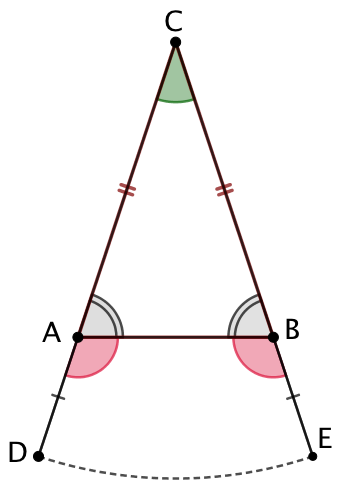
Soit un triangle ABC isocèle en C. On prolonge les côtés AC et BC. Soit D un point de la demi-droite [CA). Avec le compas, on place sur la demi-droite [CB) un point E tel que CD = CE. |
 |
 |
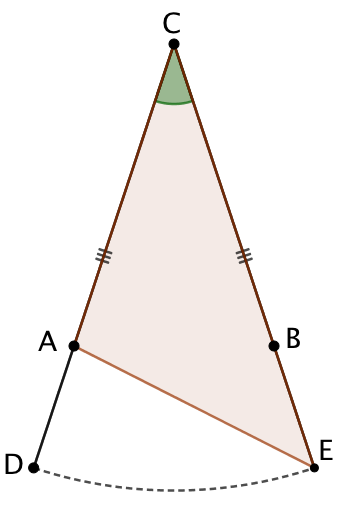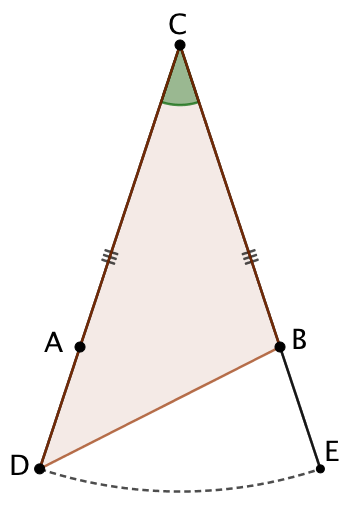
On complète la figure avec les segments [BD] et [AE]. On observe alors que les triangles CDB et CAE ont deux côtés deux à deux de même longueur : CD = CE et CA = CB. De plus ces deux triangles ont un angle en commun,  , situé entre les deux côtés deux à deux égaux. En vertu de la proposition I.4 d’Euclide, les triangles CDB et CAE sont isométriques. Ce qui permet d’affirmer que DB = AE. |
 |
 |
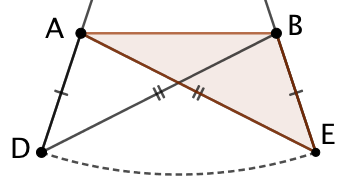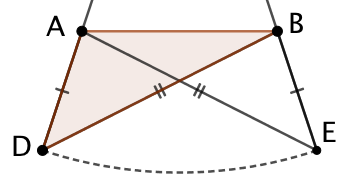Comme CA = CB et que CD = CE, on sait que AD = BE. On vient de démontrer que DB = AE. On en conclut que les triangles ADB et AEB sont isométriques. |
 |
 |
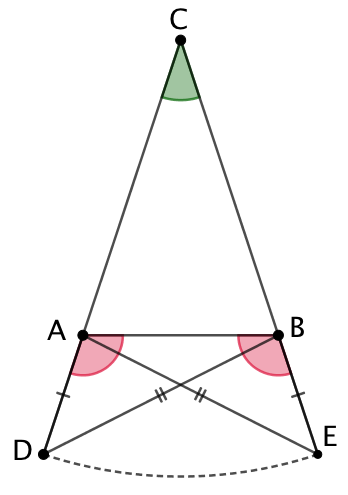Alors les angles  et  ont la même mesure.Puisque les points C, A et D sont alignés,  mais  . Donc  .
De la même manière : |
. On a démontré que 
. Par conséquent 
.Remarque : Il s’agit de la proposition I.5 des Éléments d’Euclide. La démonstration d’Euclide est un peu plus laborieuse car il n’utilise pas à ce stade la notion d’angle plat : Puisque les points C, A et D sont alignés…
