On va montrer que ![]() et que
et que ![]()
Dérivée de sinus : Soit ![]() . On va déterminer les nombres dérivés en
. On va déterminer les nombres dérivés en ![]() des fonctions sinus et cosinus.
des fonctions sinus et cosinus.
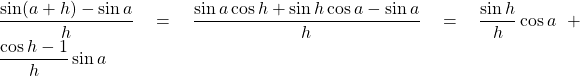 .
.
Nous savons que ![]() et que
et que ![]() .
.
Par conséquent ![]() .
.
Dérivée de cosinus : On rappelle que ![]() . Donc
. Donc ![]()
Résultats utilisés :
Ce qui est affirmé sans preuve peut être nié sans preuve (Euclide). Le but ultime n'est rien, le mouvement est tout (Eduard Bernstein)
On va montrer que ![]() et que
et que ![]()
Dérivée de sinus : Soit ![]() . On va déterminer les nombres dérivés en
. On va déterminer les nombres dérivés en ![]() des fonctions sinus et cosinus.
des fonctions sinus et cosinus.
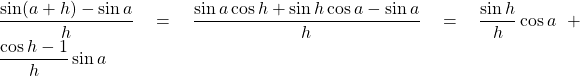 .
.
Nous savons que ![]() et que
et que ![]() .
.
Par conséquent ![]() .
.
Dérivée de cosinus : On rappelle que ![]() . Donc
. Donc ![]()
Résultats utilisés :