Les fonctions sinus et cosinus dérivables en 0

L’objectif est de démontrer que

  • \lim \limits_{x \to 0} \dfrac{ \sin x}{x} = 1, ou ce qui revient au même, que la fonction sinus est dérivable en 0 de nombre dérivé 1.
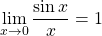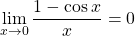  • \lim \limits_{x \to 0} \dfrac{ 1 - \cos x}{x} = 0, ou ce qui revient au même, que la fonction cosinus est dérivable en 0 de nombre dérivé 0.

Rappel d’une propriété : L’aire d’un secteur est proportionnel à son angle d’ouverture. Un disque entier correspondant à un angle de mesure 2 \pi et vaut \pi r^2. Alors un secteur d’angle \alpha (exprimé en radians) a une aire de \dfrac{\alpha \times \pi r^2}{2 \pi} = \dfrac{\alpha r^2}{2}.

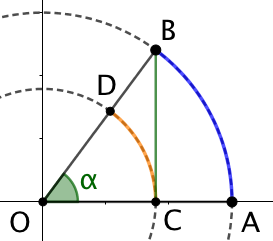
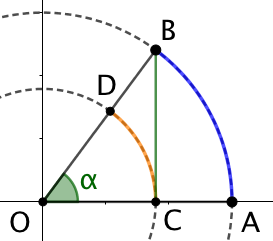
Nombre dérivé en 0 de la fonction sinus : Considérons le cercle trigonométrique de centre 0 et passant par A et B. La mesure de l’angle \widehat{AOC} est \alpha \in ]0 ; \dfrac{\pi}{2} [. Soient C le projeté orthogonal de B sur (OC). Enfin considérons un cercle de centre O et de rayon OC. Ce cercle coupe [OB] en D On a :

    \[ OA = OA = 1 \qquad \sin \alpha = \dfrac{CB}{OB} = CB \qquad \qquad \cos \alpha = \dfrac{OC}{OB} = OC \]

L’aire du secteur OCD est : \alpha \dfrac{OC^2}{2} = \dfrac{\alpha}{2} \cos^2 \alpha.

L’aire du triangle rectangle OCB est : \dfrac{OC \times CB}{2} = \dfrac{ \cos \alpha \sin \alpha}{2}.

L’aire du secteur OAB est : \dfrac{ \alpha }{2}.

On a bien évidemment les inégalités suivantes : \dfrac{\alpha}{2} \cos^2 \alpha < \dfrac{ \cos \alpha \sin \alpha}{2} < \dfrac{ \alpha }{2}.

Après simplification par \dfrac{2}{\alpha \cos \alpha} et sachant que \cos \alpha \in ]0 ; 1[, il vient \cos \alpha < \dfrac{\sin \alpha}{\alpha} < \dfrac{1}{\cos \alpha}.

La passage aux limites pour \alpha tendant vers 0+ implique que \lim \limits_{\alpha \to 0+} \dfrac{ \sin \alpha}{\alpha} = 1.

Sachant que la fonction sinus est impaire, on peut en déduire que \lim \limits_{\alpha \to 0-} \dfrac{ \sin \alpha}{\alpha} = 1.

Nombre dérivé en 0 de la fonction cosinus : 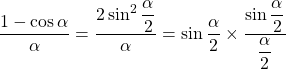 \dfrac{ 1 - \cos \alpha}{\alpha} = \dfrac{2 \sin^2 \dfrac{\alpha}{2}}{\alpha} = \sin \dfrac{\alpha}{2} \times \dfrac{\sin \dfrac{\alpha}{2}}{\dfrac{\alpha}{2}}.

On sait que \lim \limits_{\alpha \to 0} \dfrac{ \sin \alpha}{\alpha} = 1 et que \lim \limits_{\alpha \to 0} \sin \alpha}= 0. Le changement de variable de \alpha en \dfrac{\alpha}{2} conserve ces limites. Par conséquent \lim \limits_{\alpha \to 0} \dfrac{ 1 - \cos \alpha}{\alpha}= 0

Print Friendly, PDF & Email