 On démontre que
On démontre que ![]() et que
et que ![]() .
.
Explications :
On sait que ![]() et que
et que ![]()
On utilise la formule de Moivre : ![]() .
.
On développe le membre de gauche de cette égalité en ne conservant que sa partie imaginaire qui doit être égale à ![]() :
:
![]() .
.
En posant ![]() et
et ![]() , cette équation s’écrit :
, cette équation s’écrit : ![]() .
.
Comme a n’est pas nul, il vient : ![]() .
.
En posant ![]() , on obtient une équation du second degré :
, on obtient une équation du second degré : ![]() .
.
Les deux solutions de cette équation : ![]()
Ce qui donne pour ![]() , dont des valeurs approchées sont 0,59 et 0,95.
, dont des valeurs approchées sont 0,59 et 0,95.
Comme ![]() et que la fonction sinus est croissante sur
et que la fonction sinus est croissante sur ![]() alors
alors ![]() , et nécessairement
, et nécessairement ![]() est
est ![]() .
.
Sachant que ![]() , on obtient
, on obtient ![]() .
.
On peut obtenir une expression plus simple pour ![]() :
: 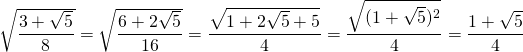 .
.
On remarque que ![]() , le nombre d’or.
, le nombre d’or.
