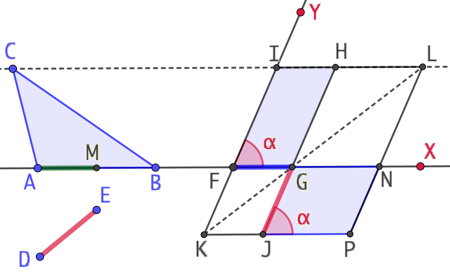
 Soit un triangle ABC et un angle
Soit un triangle ABC et un angle ![]() de mesure
de mesure ![]() . On veut construire un parallélogramme de même aire que celle de ABC, dont l’un des angles est
. On veut construire un parallélogramme de même aire que celle de ABC, dont l’un des angles est ![]() et dont l’un des côtés a une longueur DE donnée.
et dont l’un des côtés a une longueur DE donnée.
Construction :
- On construit le parallélogramme FGHI de même aire que ABC et dont l’un des angles est
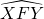 en utilisant la proposition I.42 d’Euclide.
en utilisant la proposition I.42 d’Euclide. - On trace sur la droite (GH) le segment [GJ] de longueur DE.
- On trace la droite parallèle à (FX) passant par J. Elle coupe la droite (FI) en K.
- On trace la droite (KG). Elle coupe la droite (IH) en L.
- On trace la droite parallèle à (FY) passant par L. Elle coupe (FG) en N et (KJ) en P. Le parallélogramme GJPN est le parallélogramme recherché.
Explications :
Comme la construction ne fait intervenir que des droites parallèles, il est facile de montrer que IKPL est un parallélogramme dont l’une des diagonales est (KL).
La construction fait apparaître deux parallélogrammes FGHI et GJPN qui possèdent un sommet commun sur la diagonale (KL). D’après la proposition I.43 d’Euclide, on sait que ces deux parallélogrammes ont la même aire. Donc GJPN a la même aire que ABC et l’un de ses côtés, GJ, a une longueur égale à DE.
Par construction (IF) et (GJ) sont parallèles, (FG) et (JP) sont parallèles, alors les angles ![]() et
et ![]() ont la même mesure
ont la même mesure ![]() .
.
Remarque : Il s’agit de la proposition I.44 des Éléments d’Euclide.
