5 page 70
Développe les expressions suivantes :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
6 page 70
Factorise les expressions suivantes
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
9 page 70
Réduis les expressions suivantes :
11 page 70
Développe et réduis :
![]()
![]()
13 page 70
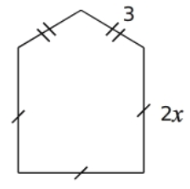 Détermine le périmètre de la figure ci-contre en fonction de
Détermine le périmètre de la figure ci-contre en fonction de ![]()
17 page 71
Développe les expressions suivantes :
![]()
![]()
![]()
![]()
25 page 71
 Un commerçant reçoit 12 caisses contenant des oeufs protégés par du carton. Chaque caisse vide pèse 1,5 kg et contient 200 g de carton. Calcule de deux façons différentes la masse totale d’emballage.
Un commerçant reçoit 12 caisses contenant des oeufs protégés par du carton. Chaque caisse vide pèse 1,5 kg et contient 200 g de carton. Calcule de deux façons différentes la masse totale d’emballage.
31 page 72
Factorise les expressions suivantes :
![]()
![]()
![]()
![]()
45 page 73
Réduis les expressions suivantes :
![]()
![]()
![]()
![]()
50 page 73
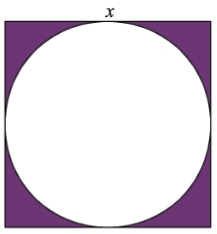 La figure ci-contre est composée d’un carré de côté
La figure ci-contre est composée d’un carré de côté ![]() et d’un disque tangent à ce carré.
et d’un disque tangent à ce carré.
L’aire de la partie violette est l’aire du carré de côté ![]() moins l’aire du disque de rayon
moins l’aire du disque de rayon ![]() .
.
a) Pour ![]() , reproduis cette figure puis calcule l’aire de la partie violette.
, reproduis cette figure puis calcule l’aire de la partie violette.
L’aire du carré est ![]() .
.
Le rayon du disque est 3. Donc son aire est ![]() .
.
L’aire de la partie violette est alors : ![]() .
.
b) Exprime l’aire du carré en fonction de ![]() .
.
L’aire du carré de côté ![]() est
est ![]() .
.
c) Exprime l’aire du disque en fonction de ![]() .
.
Le rayon du disque blanc est ![]() . Donc son aire est
. Donc son aire est ![]() .
.
d) Exprime alors l’aire de la partie violette en fonction de ![]() . Factorise puis réduis cette expression. Appelons
. Factorise puis réduis cette expression. Appelons ![]() cette aire.
cette aire.
![]() .
.
