 L’angle externe
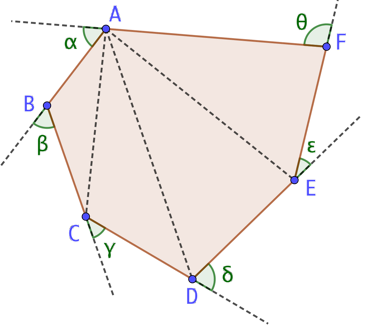
L’angle externe ![]() est l’angle de sommet A et de côté [AB) et la prolongation à partir de A du côté précédent [FA). On définit les autres angles externes de la même façon en tournant dans le même sens. La somme des mesures des angles externes d’un polygone est
est l’angle de sommet A et de côté [AB) et la prolongation à partir de A du côté précédent [FA). On définit les autres angles externes de la même façon en tournant dans le même sens. La somme des mesures des angles externes d’un polygone est ![]() .
.
Explications :
Supposons que le polygone a ![]() côtés On le découpe en
côtés On le découpe en ![]() triangles ayant tous A comme sommet. On sait par ailleurs que la somme des mesures des angles d’un polygone est
triangles ayant tous A comme sommet. On sait par ailleurs que la somme des mesures des angles d’un polygone est ![]() .
.
Pour le point A : ![]() est égal à la différence entre
est égal à la différence entre ![]() et la somme des mesures de tous les angles de sommet A.
et la somme des mesures de tous les angles de sommet A.
Pour les ![]() autres sommets du polygone : l’angle externe est égal à la différence entre
autres sommets du polygone : l’angle externe est égal à la différence entre ![]() et la mesure de l’angle du polygone pour ce sommet. Ainsi
et la mesure de l’angle du polygone pour ce sommet. Ainsi ![]() .
.
Donc ![]() .
.
