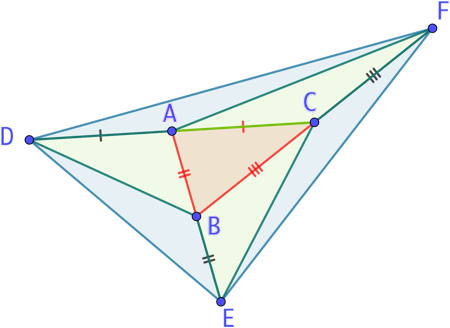
Étant donné un triangle quelconque ABC, on trace six autres triangles possédant la même aire que le premier :
- On place le point D symétrique de C par rapport à A.
- Puis on place E symétrique de A par B.
- Et enfin F symétrique de B par C.
- Les triangles trois triangles verts et les trois triangles bleus ont la même aire que le triangle ABC.
Explications :
D est le symétrique de C par rapport à A donc A est le milieu du segment [CD, ou dit autrement AD = AC. Or, les triangles FAD et FAC ont un sommet F en commun et deux bases [AD] et [AC]. On peut alors affirmer que FAD et FAC on la même aire.
On démontrerait de la même façon que BAD et BED ont la même aire, et que CEB et CEF ont la même aire.
Sachant que CB = CF et que les triangles ABC et FAC ont un sommet commun A, il vient que des deux triangles ont la même aire. Comme FAC et FAD avaient la même aire, on en conclut que FAC et FAD ont la même aire que ABC.
En reprenant la même démonstration pour les triangles BAD et BEC comparés à ABC, on finit par démonter que les sept triangles ont la même aire.
