PREMIER CAS
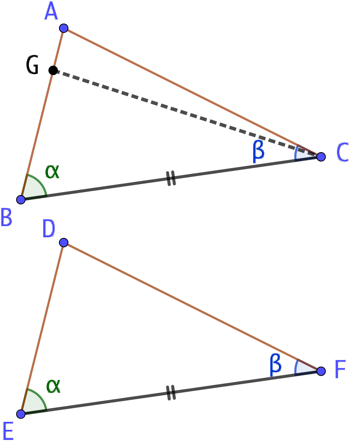
Soient deux triangles ABC et DEF possédant deux angles de même mesure et tels que les côtés entre les angles aient la même longueur, alors les deux triangles sont isométriques.
Explications :
Puisque BC = EF, si on place le point E sur B, le point F sera sur C. Si on pose le segment [ED] à partir de B et faisant avec la (BC) un même angle 
, le point D sera sur la droite (BA).
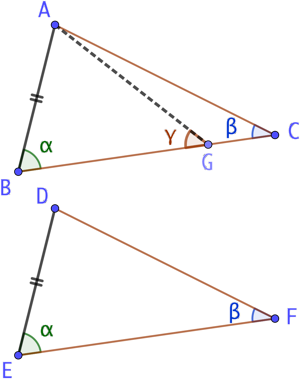
Raisonnons par l’absurde et supposons que ED < BA. Alors le point D sera positionné sur un point G tel que BG = ED. Alors 
ce qui est impossible puisque les triangles GBC et DEF sont isométriques, ce qui implique que 
.
Donc BA = ED. Comme BC = EF et 
, on peut affirmer que les triangles ABC et DEF sont isométriques.
DEUXIÈME CAS
Soient deux triangles ABC et DEF possédant deux angles de même mesure et tels que deux côtés de même longueur mais qui ne soient pas entre les deux angles égaux, alors les deux triangles sont isométriques.
Explications :
Comme BA = ED, si on place E sur B, le point D se posera sur A. Comme , (EF) se posera sur (BC). Raisonnons par l’absurde et supposons que ED < BC et que le point F se placera sur G.
est un angle extérieur au triangle AGB donc 
. Or les triangles ABG et DEF sont isométriques. Donc 
Conclusion : EF = BC. Comme BA = ED et , on peut affirmer que les triangles ABC et DEF sont isométriques.
Remarque : Il s’agit de la proposition I.26 des Éléments d’Euclide.
