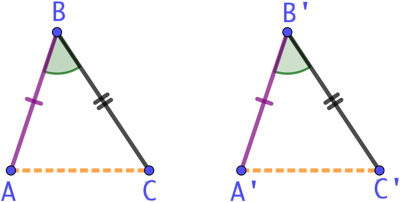
Soient deux triangles ayant deux côtés deux à deux de même longueur et un angle entre ces deux côtés de même mesure. Alors les deux derniers côtés sont de même longueur.
Explications : On sait que 
, et 
.
Si on place le segment [BA] sur [B’A’] à partir du point B’, le point A va recouvrir le point A puisque 
, et comme , le point C va recouvrir le point C’ puisque 
. Donc nécessairement le segment [AC] va recouvrir exactement le segment [A’C’].
Ainsi les distances AC et A’C’ sont égales et on aura les égalités d’angles homologues : 
et 
. Conclusion : les deux triangles sont isométriques.
Remarque : Il s’agit de la proposition I.4 des Éléments d’Euclide.
