I – Volume d’un solide

Définition

Le volume d’un solide est la mesure de l’espace occupé par ce solide, dans une unité de volume donnée.

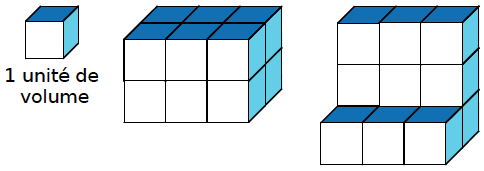Exemple : Pour trouver le volume de chaque solide, il suffit de compter le nombre d’unités de volume qui le constituent. Les deux solides ont pour volume 12 (en unités de volume) alors qu’ils n’ont pas la même forme.

II – Unités de volume et de capacité

1) Unités de volume

Définition

L’unité de volume usuelle est le mètre cube (noté m³), qui représente le volume d’un cube de côté 1 m. On utilise aussi : ses multiples (dam³, hm³, km³) et ses sous-multiples (dm³, cm³, mm³).

Exemples :

1 cm³ est le volume d’un cube d’un centimètre de côté.
1 mm³ est le volume d’un cube d’un millimètre de côté.
Dans 1 cm³, il y a 1 000 mm³.

Règles

Pour passer d’une unité de volume à l’unité immédiatement inférieure, on multiplie par 1 000.
Pour passer d’une unité de volume à l’unité immédiatement supérieure, on divise par 1 000.

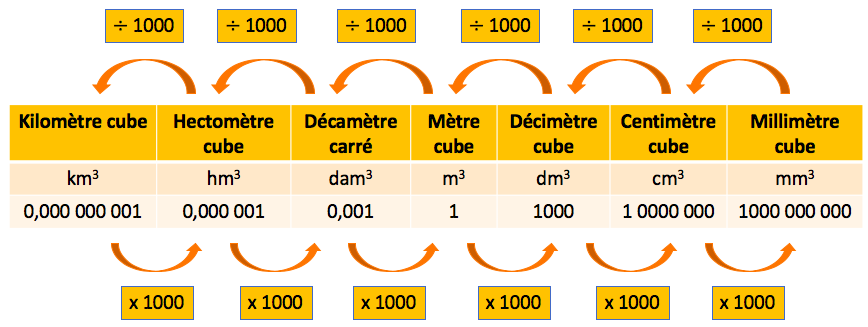
Exemples :

53 dam³ = 53 000 m³
0,36 m³ = 360 dm³
5 dm³ = 0,005 m³

Autres unités fréquemment utilisées : Pour mesurer des volumes de liquide, on utilise :

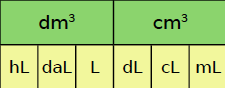le litre : 1 L = 1 dm³
l’hectolitre : 1 hL = 100 L
le décilitre : 1 dL = 100 cm³
le centilitre : 1 cL = 10 cm³
le mililitre : 1 mL = 1 cm³

Exemples :

15 L = 0,15 hL
3,5 L = 350 cL
3 mL = 0,3 cL

III – Volume d’un parallélépipède rectangle

ATTENTION : Pour calculer un volume, les dimensions doivent être exprimées dans la même unité de longueur.

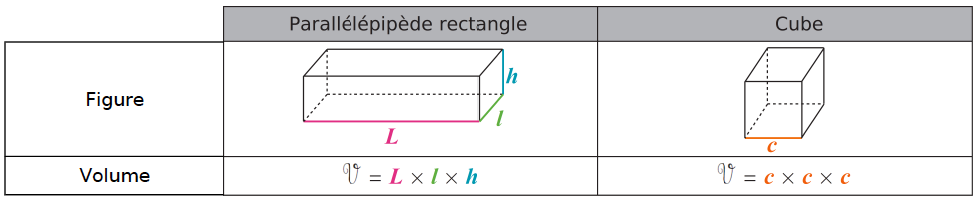
Exemple : Calcule le volume d’un pavé droit de 32 mm de longueur, 2,5 cm de largeur et 0,4 dm de hauteur.

On écrit la formule : $V = L \times l :times h$
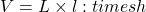
On remplace par les données numériques exprimées dans la même unité : 32 mm = 3,2 cm et 0,4 dm = 4 cm.
Le volume du pavé droit est 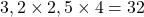$3,2 \times 2,5 \times 4 = 32$ cm³.