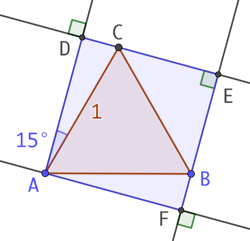
Un triangle équilatéral dans un carré

Il s’agit de trouver le plus petit carré de côté de longueur a dans lequel on puisse inscrire un triangle équilatéral de côté de longueur 1 unité.

On peut d’abord tenter plusieurs essais à la main qui permettent assez rapidement de faire ressortir une symétrie dans le résultat : les angles CAD et FAB ont très probablement la même mesure. Pour s’en convaincre :

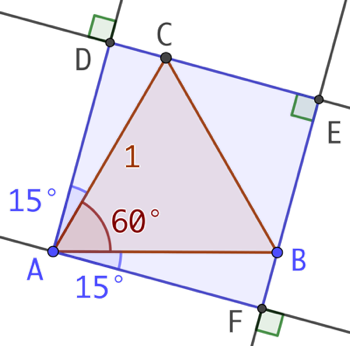
Le cosinus de CAD vaut AD / AC, soit a puisque AD = a et AC = 1. Le cosinus de FAB = AF / AB = 1. Les deux angles étant aigus et de même cosinus, ils ont la même mesure ß.

En observant les 3 angles de sommet A, il vient : ß + 60 + ß = 90. d’où 2ß = 90 – 60, soit ß = 15°. Donc les côtés du carré mesurent cos 15°.

Rappel trigonométrique : a = cos2ß = (1 + cos2ß) / 2.

  • 2ß = 30° donc cos2ß = √3/2
  • cos2ß = (1 +√3/2) / 2 = (2 + √3) / 4
  • cosß = √(2+ √3) / 2

Valeur approchée de a : 0,97


Construction :

  1. On trace le triangle équilatéral ABC de côté 1.
  2. On trace une demi droite faisant un angle de 15° avec [AC].
  3. On trace la perpendiculaire à cette demi-droite qui passe par C. On note D le point d’intersection.
  4. On trace la perpendiculaire à (DC) qui passe par B. On note E le point d’intersection avec (DE).
  5. On trace la perpendiculaire à (EB) qui passe par A. On note F le point d’intersection.
  6. Le carré ADEF est celui que l’on recherchait.
Print Friendly, PDF & Email