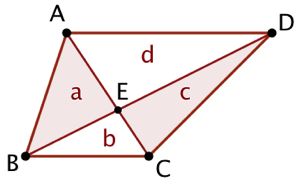
Soient le trapèze ABCD avec (AD) et (BC) parallèles et E le point d’intersection de ses deux diagonales. Alors les triangles ABE et DEC ont la même aire.
Explications :
Soient a, b et c les aires respectives des triangles ABE, EBC et DEC.
Comme (AD) // (BC), les triangles ABC et DBC qui partage la même base [BC] ont la même aire. Donc a + b = c + b. Il vient immédiatement que a = c.
Le même raisonnement peut être fait en remplaçant c par d, l’aire de AED.
