Un quadrilatère dans un carré

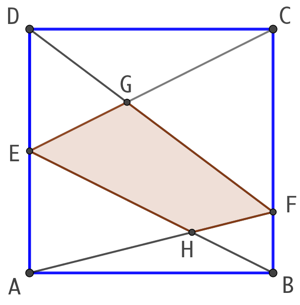
ABCD est un carré de côtés mesurant une unité. E est le milieu du segment [AD] et F est un point du segment [BC] situé à un quart d’unité de B. G est le point d’intersection des droites (DF) et (EC). H est le point d’intersection des droites (EB) et (AF). On veut déterminer l’aire du quadrilatère EHFG.

Explications :

L’aire de EHFG s’obtient en retirant de DAF les aires des triangles DEG et EAH.

L’aire du triangle DAF est $\dfrac{1}{2}$ .

Le théorème de Thales permet de déterminer les aires de DEG et EAH. On fait apparaître sur la figure les hauteurs de ces triangles.

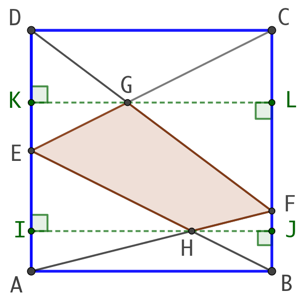Triangle DEG : On observe que 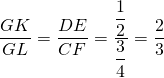$\dfrac{GK}{GL} = \dfrac{DE}{CF} = \dfrac{ \dfrac{1}{2}}{ \dfrac{3}{4}} = \dfrac{2}{3}$ . Ce qui donne $GL = \dfrac{3}{2} GK$ .

Or $GK + GL = 1 = GK + \dfrac{3}{2} GK = \dfrac{5}{2} GK$ . Donc $GK = \dfrac{2}{5}$ .

Ainsi l’aire de DEG est : $\dfrac{1}{2} \times \dfrac{1}{2} \times \dfrac{2}{5} = \dfrac{1}{10}$ .

Triangle EAH : On observe que 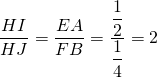$\dfrac{HI}{HJ} = \dfrac{EA}{FB} = \dfrac{ \dfrac{1}{2}}{ \dfrac{1}{4}} = 2$ . Ce qui donne $HJ = \dfrac{1}{2} HI$ .