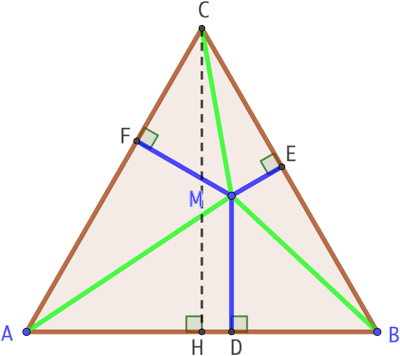
 Étant donnés un triangle ABC et un point M placé à l’intérieur du triangle, La somme des distances de ce point aux côtés du triangle est constante et égale à la hauteur du triangle :
Étant donnés un triangle ABC et un point M placé à l’intérieur du triangle, La somme des distances de ce point aux côtés du triangle est constante et égale à la hauteur du triangle : ![]() .
.
Explications :
On calcule l’aire du triangle ABC de deux façons différentes.
Par définition c’est ![]() .
.
C’est aussi la somme des aires des trois triangles : MAB, MBC et MCA.
La hauteur de MAB issue de M est MD, donc l’aire de MAB est ![]() . On trouve facilement que les aires respectives de MBC et MCA sont
. On trouve facilement que les aires respectives de MBC et MCA sont ![]() et
et ![]() .
.
On peut alors écrire l’équation : ![]() . Or ABC est un triangle équilatéral donc
. Or ABC est un triangle équilatéral donc ![]() . L’équation devient :
. L’équation devient : ![]() . Ce qui donne après simplification :
. Ce qui donne après simplification : ![]() .
.
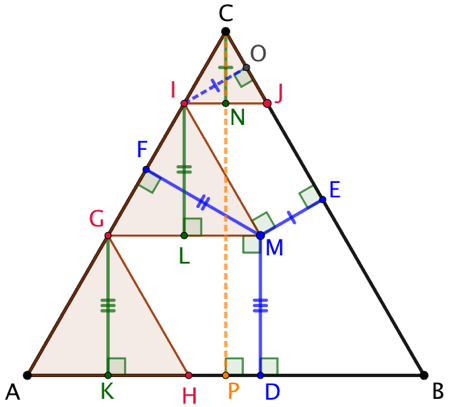 Autre approche :
Autre approche :
Ce raisonnement s’appuie sur le fait que les hauteurs d’un triangle équilatéral ont la même longueur.
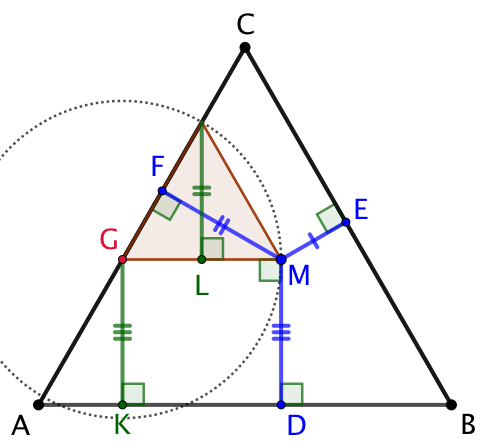
Soit G l’intersection de la droite passant par M et parallèle à (AD). On construit le triangle équilatéral GAH de côté de longueur AG. Soit K le projeté orthogonal de G sur (AD). Alors MD = GK.
On construit le triangle équilatéral IGM de côté de longueur GM. Soient F le projeté orthogonal de M sur (AC) et L le projeté orthogonal de I sur (GM). Alors MF = IL.
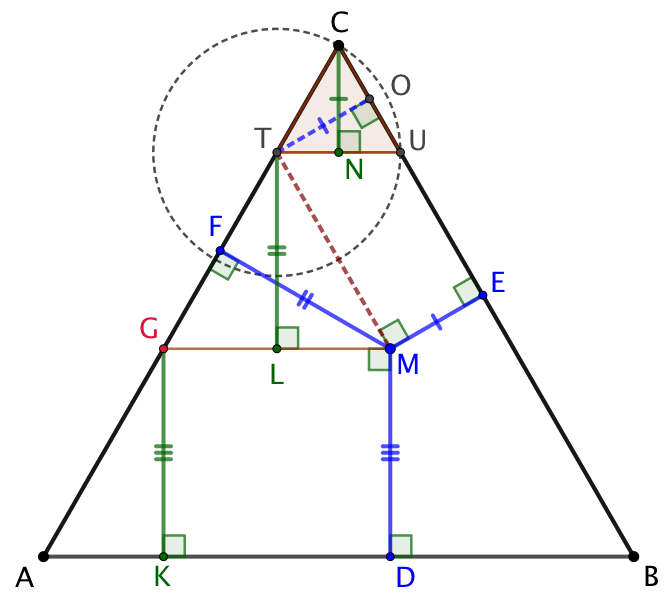
On construit le triangle équilatéral CIJ de côté de longueur CI. Soit O le projeté orthogonal de I sur (BC). ME = IO car les droites (IM) et (CE) sont parallèles. En effet les angles correspondants ![]() et
et ![]() sont de même mesure.
sont de même mesure.
Soit N le projeté orthogonal de C sur (IJ). Alors CN = IO = ME.
Conclusion : MD + MF + ME = GC + IL + CN = CP
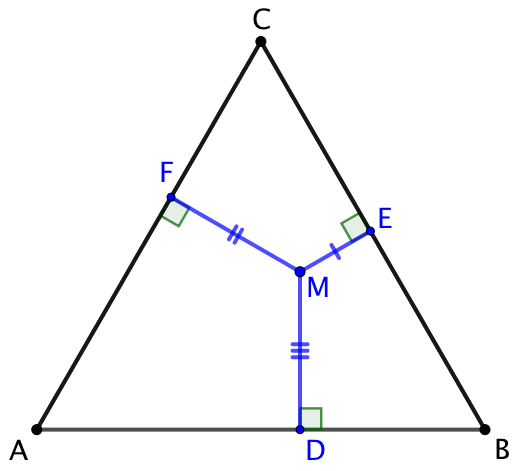
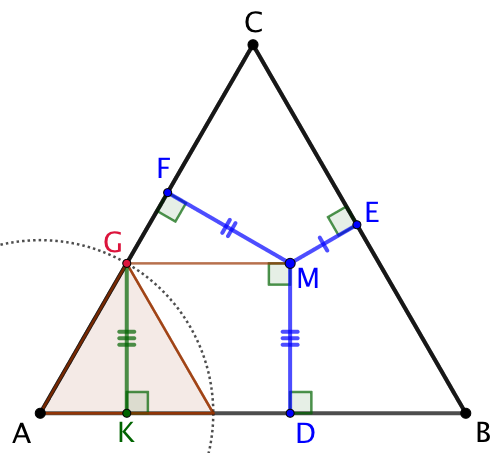
Même approche (profs without words) :
 |
 |
 |
 |
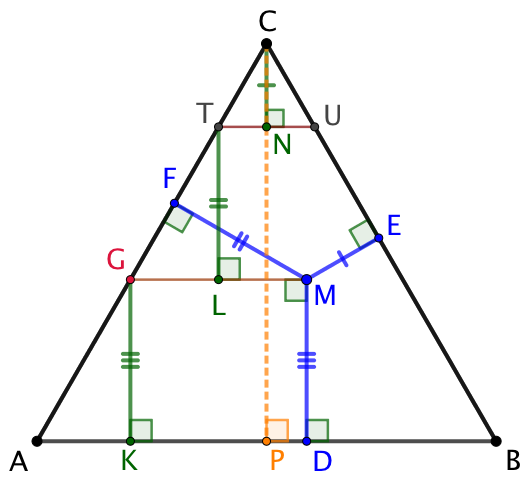 |
CP = CN + TL + GK |
