Les basiques
![]()
![]()
![]()
Les produits
![]()
![]()
Les sommes
![]()
![]()
Changement de variable
![]()
Fonctions réciproques
![]()
![]()
![]()
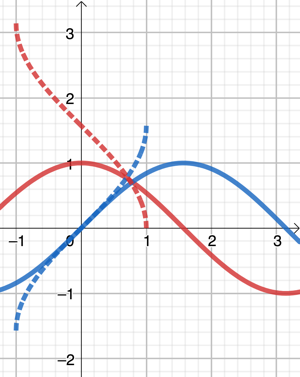
Ce qui est affirmé sans preuve peut être nié sans preuve (Euclide). Le but ultime n'est rien, le mouvement est tout (Eduard Bernstein)

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
