 On construit un triangle inscrit dans un cercle ainsi :
On construit un triangle inscrit dans un cercle ainsi :
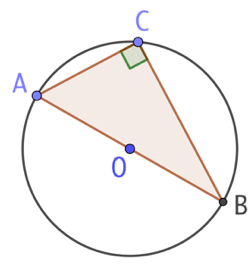
1er cas : le cercle est donné
- On trace un diamètre [AB] de ce cercle.
- On choisit un point C quelconque sur ce cercle.
- Le triangle ABC est rectangle en C.
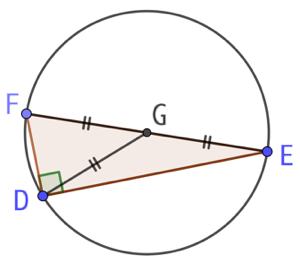
2ème cas : le triangle rectangle est donné, DEF rectangle en D
- On place le milieu G de l’hypoténuse [EF].
- On trace le cercle de centre G et passant par D. Le triangle DEF est bien inscrit dans ce cercle.
 On note que dans un triangle rectangle, la distance entre le milieu de l’hypoténuse et le sommet de l’angle droit est égale à la moitié de la longueur de l’hypoténuse.
On note que dans un triangle rectangle, la distance entre le milieu de l’hypoténuse et le sommet de l’angle droit est égale à la moitié de la longueur de l’hypoténuse.
Explications :
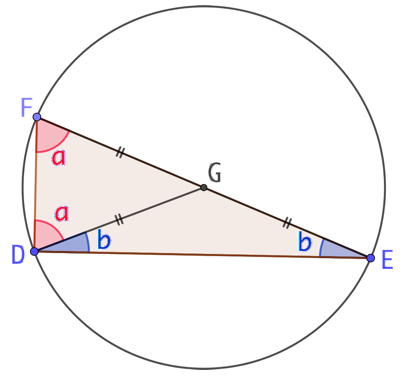
DFG est un triangle isocèle puisque deux de ses côtés sont des rayons du cercle. Les deux angles à la base sont de même mesure a.
De même DEG possède deux angles à la base de même mesure b.
La somme des mesures des 3 angles du triangle DEF est ![]() . Donc
. Donc ![]() .
.
 Or
Or ![]() est la mesure de l’angle
est la mesure de l’angle ![]() , ce qui démontre que cet angle est droit et que le triangle est rectangle.
, ce qui démontre que cet angle est droit et que le triangle est rectangle.
Remarque : Il s’agit d’une partie de la proposition III.31 des Éléments d’Euclide.
Application : Construction d’un triangle dont on connaît la base et deux hauteurs
RÉCIPROQUE
Le diamètre du cercle circonscrit d’un triangle rectangle est l’hypoténuse de ce triangle.
Explication n°1 :
